(Qiu, Wu and Pedram)
This case study is based on a CTMC model of a 4 state Fujitsu disk drive taken from [QWP99]. As in [QWP99], we suppose that request inter-arrival distribution has the same (mean) expected value and equals 0.72, and that the maximum size of the service request queue (SRQ) is 20.
In this model the Service Provider (SP) has four states which are shown below.
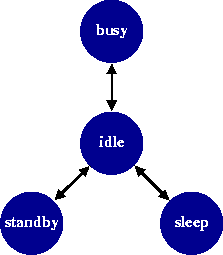
The SP makes a transition from idle to busy whenever a request arrives for service. Similarly, it makes a transition from busy to idle whenever it finishes the service of a request. Transitions between sleep, standby and idle are controlled by the PM. The only condition we impose on the PM is that, when the SRQ is full and the SP is in sleep or standby, the PM switches the SP on, i.e. the SP moves to idle. The performance of the SP is given in the following tables where the data is taken from [QWP99]:
Average power consumption and service times of the SP
| sleep | standby | idle | busy | average power | 0.13 | 0.35 | 0.95 | 2.15 | average service time | 0 | 0 | 0 | 0.008 |
Average energy consumption values for state transitions of the SP
| sleep | standby | idle | busy | |
| sleep | 0 | 5.1 | 7 | - |
| standby | 0.006 | 0 | 2 | - |
| idle | 0.067 | 0.001 | 0 | 0 |
| busy | - | - | 0 | 0 |
Average transition times for state transitions of the SP
| sleep | standby | idle | busy | |
| sleep | 0 | 0.6 | 1.6 | - |
| standby | 0.3 | 0 | 1.2 | - |
| idle | 0.67 | 0.4 | 0 | 0 |
| busy | - | - | 0 | 0 |
The module representing the SP is given below. Note that the actions corresponding to local changes of the SP synchronise with the PM, whereas the transitions corresponding to the service and arrival of requests synchronise with the SRQ.
// SERVICE PROVIDER // assume: SP automatically // moves from idle to busy when ever a request arrives // moves from busy to idle when ever a request is served // rates of local state changes const double sleep2standby=10/6; const double sleep2idle=10/16; const double standby2sleep=10/3; const double standby2idle=10/12; const double idle2sleep=100/67; const double idle2standby=10/4; // rate of service const double service=1000/8; module SP sp : [0..3]; // 0 - sleep, 1 - standby, 2 - idle, 3 - busy // SLEEP TO STANDBY [sleep2standby] sp=0 -> sleep2standby : (sp'=1); // SLEEP TO IDLE [sleep2idle] sp=0 & q=0 -> sleep2idle : (sp'=2); // go to idle [sleep2idle] sp=0 & q>0 -> sleep2idle : (sp'=3); // start serving immediately // STANDBY TO SLEEP [standby2sleep] sp=1 -> standby2sleep : (sp'=0); // STANDBY TO IDLE [standby2idle] sp=1 & q=0 -> standby2idle : (sp'=2); // go to idle [standby2idle] sp=1 & q>0 -> standby2idle : (sp'=3); // start serving immediately // IDLE TO SLEEP (only if queue is empty) [idle2sleep] sp=2 & q=0 -> idle2sleep : (sp'=0); // IDLE TO STANDBY (only if queue is empty) [idle2standby] sp=2 & q=0 -> idle2standby : (sp'=1); // idle to serve (add loops when not in idle) [request] sp=2 -> (sp'=3); [request] sp!=2 -> true; // SERVICE REQUESTS (move to idle if queues empty) [serve] sp=3 & q>1 -> service : (sp'=3); [serve] sp=3 & q=1 -> service : (sp'=2); endmodule
Since there is only one queue, the SRQ and the SR can be combined into the following module:
// SERVICE REQUESTER AND SERVICE REQUEST QUEUE const int QMAX=20; // size of queue const double request=100/72; // rate of arrivals module SRQ q : [0..QMAX]; [request] true -> request : (q'=min(q+1,QMAX)); // request arrives [serve] q>0 -> (q'=q-1); // request served endmodule
Given a performance constraint (average number of requests awaiting service), we construct the optimal policy which minimises the average power consumption while satisfying the performance constraint. We obtained these policies by constructing the generator matrix of the system in PRISM and then, from this, constructing a linear optimization problem which we solve with Maple using its Simplex package.
Below, we list the policies obtained under a selection of different different performance constraints where, if no behaviour is specified, the choice of the policy is to do nothing (stay in the same state).
| Constraint | Policy | |
| average number of requests awaiting service <=20 |
go from idle to standby when the SRQ is empty go from standby to idle when the SRQ is full |
|
| average number of requests awaiting service <= 10 |
go from idle to standby when the SRQ is empty go from standby to idle when the SRQ is full when the SRQ is of size N-1 and in standby: move to idle with probability 0.120879 stay in standby with probability 0.879121 | |
| average number of requests awaiting service <= 5 |
go from idle to standby when the SRQ is empty go from standby to idle when the SRQ >=10 when the SRQ is of size 9 and in standby: move to idle with probability 0.607453 stay in standby with probability 0.392547 | |
| average number of requests awaiting service <= 1 |
go from standby to idle when the SRQ >=8 when the SRQ is empty: move to standby with probability 0.043289 stay in idle with probability 0.956711 | |
| average number of requests awaiting service <= 0.25 |
go from standby to idle when the SRQ >=8 when the SRQ is empty: move to standby with probability 0.008837 stay in idle with probability 0.991163 | |
| average number of requests awaiting service <= 0.1 |
go from standby to idle when the SRQ >=8 when the SRQ is empty: move to standby with probability 0.003187 stay in idle with probability 0.996813 |
It is then straightforward to define each policy in PRISM as a module. To illustrate this we give the module for the policy with performance constraint 1.
// POWER MANAGER module PM p : [0..1]; // never in sleep so prevent transitions to and from sleep [sleep2standby] false -> true; [sleep2idle] false -> true; [standby2sleep] false -> true; [idle2sleep] false -> true; // move to stand by when queue>=8 [standby2idle] q>=8 -> true; // probabilistically move to standby from idle when queue becomes empty [serve] q=1 -> 0.043289 : (p'=1); [serve] q=1 -> 0.956711 : (p'=0); // need loop for other cases [serve] q>1 -> true; // therefore perform transition when p=1 [idle2standby] p=1 -> (p'=0); // reset p to zero since a request have arrived (queue no longer empty) [request] true -> (p'=0); endmodule
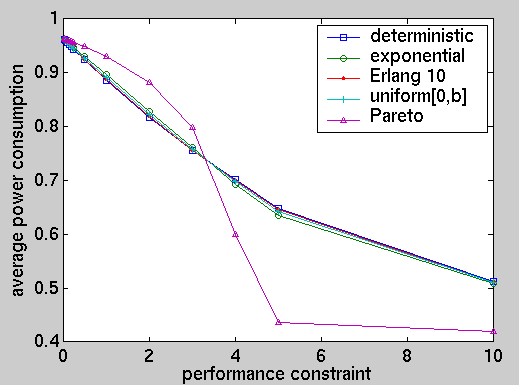
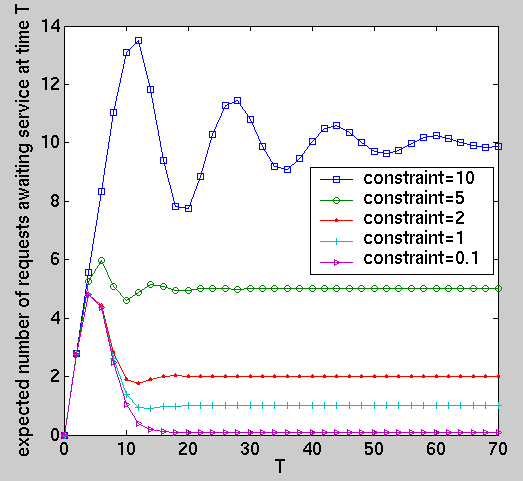
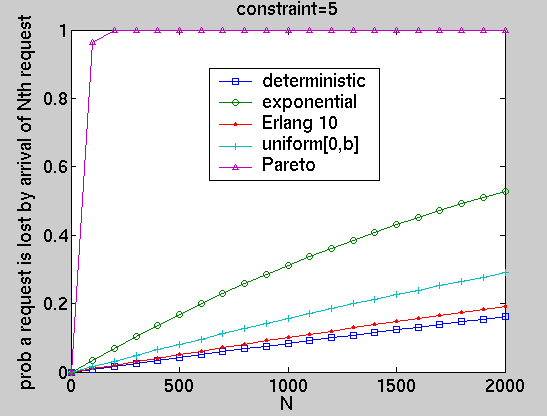
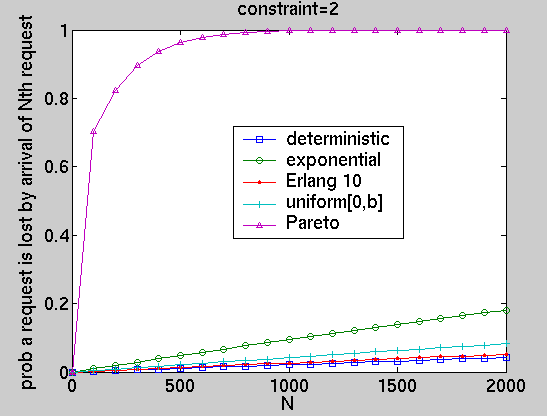
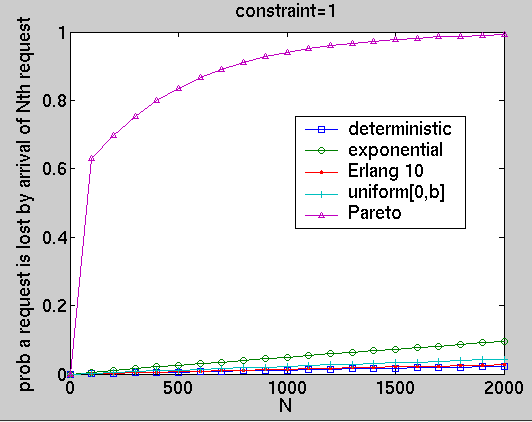
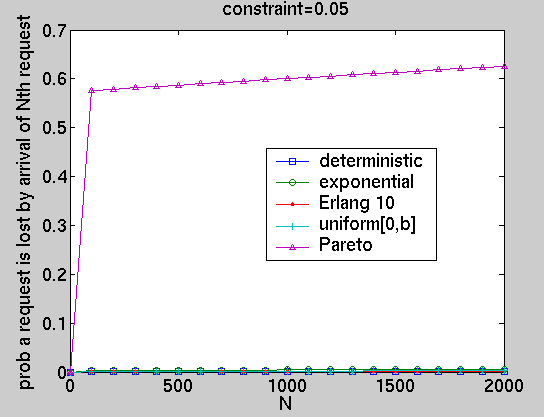
We have computed, for the optimal policies under different performance constraints and for a selection of distributions (deterministic, exponential, Erlang, uniform and Pareto), a number of different long-run and transient performance measures including the average power consumption, average number of lost customers, expected queue size at time T (when requests arrive with an exponential distribution) and the probability of a request being lost by the time the Nth request arrives.
Below, we give a number of illustrative examples. Full details of these results are available from here.