(A. Bogliolo, P. Polidori, A. Aldini, W. Moreira, P. Mendes, M. Yildiz, C. Ballester & J. Seigneur)
Related publications: [KPS13, KNPS18]
User-centric networks are designed to encourage users to act cooperatively, sharing resources or services between themselves, for example in order to provide connectivity in a mobile ad-hoc network. The effectiveness of such networks is heavily dependent on their cooperation mechanisms, which are often based on the use of incentives to behave unselfishly. In this case study, we analyse a cooperation mechanism for user-centric networks [BPA+12], which combines a reputation-based incentive, used to establish a measure of trust between users, and a virtual currency mechanism used to “buy” and “sell” services.
The basic ideas behind the cooperation mechanism of [BPA+12] can be summarised as follows. We assume a general model of providers offering services to requesters. Cooperation between users of the network (requesters and providers) is managed through a combination of reputation and virtual currency.
Reputation is captured by a discrete trust measure, denoted trustij, representing the extent to which user i trusts user j, based on previous interactions between them and the recommendations provided by the other users in the network. This is used to determine whether a service request from j is accepted by i. A trust level Tij is computed as a weighted sum:
where recsij is an “indirect” trust measure, taken as the the average value of trustkj for other users k (whereas trustkj is called a “direct” measure of trust). By default, i will decide to accept j’s request if Tij is not below a pre-specified service trust level, denoted sti. The parameter α ∈ [0,1] controls the relative influence that the direct and indirect measures of trust have on this decision.
The reputation scheme is then integrated with a virtual currency system, where services are bought and sold between users, and the cost paid to i by j for a service is a function of trustij. Assuming model parameters for minimum and maximum costs Cmin , CmX and threshold T′, the cost C(trustij) is defined as:
Procurement of a service proceeds in several phases. First, a requester j chooses a provider i and makes a request. If Tij ≥ sti, the request is accepted. In this case, the two users then “negotiate” the service cost, using the function of trustij given above. The negotiation may, however, fail: with probability ci, user i cancels the accepted request; this represents the “cooperative attitude” of the provider i. If not cancelled, the service is delivered and the requester chooses whether or not to pay the negotiated price to the provider. If payment is made, the provider increases the trust measure of the requester by one unit. If not, the measure is decreased by tdi units. On encountering a requester for the first time, a provider shares the trust measure with the other providers.
First, we consider a turn-based stochastic game model [KPS13], where a single user can either make a request to one of three service providers or buy the service directly by paying maximum price. If the user makes a request to a service provider, then the provider decides to accept or deny the request based on the user's trust measure. If the request was accepted, the provider would next decide on the price again based on the trust measure, and the user would then decide whether to pay for the service and finally the provider would update its trust measure based on whether there was a payment. This sequence of steps would have to take place before any other interactions occurred between the user and other providers.
Three trust models are considered. In the first, the trust level is decremented by 1 (td=1) when the user does not pay, decremented by 2 in the second (td=2) and reset to 0 in the third (td=inf).
// Trust models for user-centric networks from // M. Kwiatkowska, D. Parker and A. Simaitis // Strategic analysis of trust models for user-centric networks. // In: Proc. SR’13. EPTCS, vol. 112, pp. 53–60 (2013) // (have simplified the reward structures) // originally based on the trust model of // A. Bogliolo, P. Polidori, A. Aldini, W. Moreira, P. Mendes, M. Yildiz, C. Ballester, and J.-M. Seigneur. // Virtual Currency and Reputation-Based Cooperation Incentives in User-Centric Networks. // In: Proc. IWCMC-2012, Cyprus, 2012 // turn-based stochastic game smg const int K; // number of services const int td; // trust model // model parameters const double alpha_all = 0.8; // recommendation influence parameter const int st_init_all = med; // initial service trust for all providers const int reduct_all = td; // trust decrease for all providers const bool hide_all = false; // allow information hiding const double cancel = 0.05; // probability to cancel fair request const bool init_know_all = true; // sharing of initial trust const double die_prob = 0; // probability provider dies after serving a request const int cmax = 10; // maximum service cost const int cmin = 2; // minimum service cost player requester1 requester1, [pay11], [nopay11], [pay21], [nopay21], [pay31], [nopay31], [try11], [try21], [try31], [buy] endplayer player provider1 provider1, [accept11], [refuse11], [reveal11], [notreveal11] endplayer player provider2 provider2, [accept21], [refuse21], [reveal21], [notreveal21] endplayer player provider3 provider3, [accept31], [refuse31], [reveal31], [notreveal31] endplayer // probability to share information formula rev_prob = know21&(trust11>trust21) | know31&(trust11>trust31) ? 0 : 1; module requester1 x1 : [0..43] init 0; // states of the module //ns1 : [0..K] init 0; // number of requested services ps1 : [0..K] init 0; // number of payed services nps1 : [0..K] init 0; // number of unpayed services unpaid1 : bool init false; // choose service provider [try11] x1=0 & (y1+y2+y3=0) & ps1+nps1 < K -> (x1'=11) & (unpaid1'=false); [try21] x1=0 & (y1+y2+y3=0) & ps1+nps1 < K -> (x1'=21) & (unpaid1'=false); [try31] x1=0 & (y1+y2+y3=0) & ps1+nps1 < K -> (x1'=31) & (unpaid1'=false); // or buy the service off-market [buy] x1=0 & (y1+y2+y3=0) -> (x1'=41) & (unpaid1'=false); // finished sending requests [] x1=0 & (y1+y2+y3=0) & (ps1+nps1=K) -> (x1'=1) & (unpaid1'=false); [] x1=1 -> true; // reply from first requester and then decide to pay or not [accept11] x1=11 -> (x1'=12); [refuse11] x1=11 -> (x1'=13); [pay11] x1=12 -> (x1'=0) & (ps1'=min(K,ps1+1)); [nopay11] x1=12 -> (x1'=0) & (nps1'=min(K,nps1+1)) & (unpaid1'=true); [] x1=13 -> (x1'=0); // reply from second requester and then decide to pay or not [accept21] x1=21 -> (x1'=22); [refuse21] x1=21 -> (x1'=23); [pay21] x1=22 -> (x1'=0) & (ps1'=min(K,ps1+1)); [nopay21] x1=22 -> (x1'=0) & (nps1'=min(K,nps1+1)) & (unpaid1'=true); [] x1=23 -> (x1'=0); // reply from third requester and then decide to pay or not [accept31] x1=31 -> (x1'=32); [refuse31] x1=31 -> (x1'=33); [pay31] x1=32 -> (x1'=0) & (ps1'=min(K,ps1+1)); [nopay31] x1=32 -> (x1'=0) & (nps1'=min(K,nps1+1)) & (unpaid1'=true); [] x1=33 -> (x1'=0); // finish paying off-market [] x1=41 -> (x1'=0) & (ps1'=min(K,ps1+1)); endmodule label "finished" = x1=1; // requester finished // factor alpha of the cost formula const double alpha1 = alpha_all; const double alpha2 = alpha_all; const double alpha3 = alpha_all; // trust formula formula trusteq1 = min(top, !know21 & !know31 ? trust11 : floor(alpha1*trust11 + (1-alpha1)*recommend)); formula recommend = ((know21 ? trust21 : 0) + (know31 ? trust31 : 0)) / ((know21 ? 1 : 0) + (know31 ? 1 : 0)); // initial knowledge parameters const bool init_know11 = init_know_all; const bool init_know21 = init_know_all; const bool init_know31 = init_know_all; // initial trust parameters const int dt_init1 = st_init_all; // dispositional trust const int st_init1 = st_init_all; // service trust level const int trust_init1 = dt_init1; // initial trust const int tth_init1 = high; // trust threshold (see the cost formula) const int dt_init2 = st_init_all; const int st_init2 = st_init_all; const int trust_init2 = dt_init2; const int tth_init2 = high; const int dt_init3 = st_init_all; const int st_init3 = st_init_all; const int trust_init3 = dt_init3; const int tth_init3 = high; // trust reduction rates (0:NULL; 1:-1; 2:-2) const int reduct1 = reduct_all; const int reduct2 = reduct_all; const int reduct3 = reduct_all; // enable information withholding // info about requester 1 const bool hide11 = hide_all; const bool hide21 = hide_all; const bool hide31 = hide_all; module provider1 alive1 : bool init true; y1 : [0..4] init 0; // states of the module st1 : [0..level] init st_init1; // service trust level dt1 : [0..level] init dt_init1; // dispositional trust tth1 : [0..level] init tth_init1; // trust threshold (see the cost formula) trust11 : [0..level] init trust_init1; // trust towards the requester know11: bool init init_know11; // interaction flag // initiate connection with requester [try11] alive1 & (y1=0) -> ((trusteq1 < st1) ? 1 : 0) + ((trusteq1 < st1) ? 0 : 1) * cancel : (y1'=4) + (1-(((trusteq1 < st1) ? 1 : 0) + ((trusteq1 < st1) ? 0 : 1) * cancel)) : (y1'=3); [try11] !alive1 & y1=0 -> (y1'=4); // accept or refuse requester1 [accept11] (y1=3) & (trusteq1 >= st1) -> (y1'=1); //[refuse11] (y1=4) & (trusteq1 < st1) -> (y1'=0); [refuse11] (y1=4) -> (y1'=0); // settle payment with requester1 [pay11] (y1=1) -> (y1'=2) & (trust11' = (trust11 < top ? trust11+1 : top)); [nopay11] (reduct1=1) & (y1=1) -> (y1'=2) & (trust11' = (trust11 > null ? trust11-1 : null)); [nopay11] (reduct1=2) &(y1=1) -> (y1'=2) & (trust11' = (trust11 > null ? trust11-2 : null)); [nopay11] (reduct1=0) & (y1=1) -> (y1'=2) & (trust11'=null); // decide to reveal info about requester to other providers or not [reveal11] (y1=2) -> (1-die_prob) * rev_prob : (y1'=0) & (know11'=true) + (1-die_prob) * (1-rev_prob) : (y1'=0) & (know11'=false) + die_prob : (y1'=0) & (alive1'=false) & (trust11'=trust_init1) & (know11'=false); [notreveal11] hide11 & (y1=2) -> (y1'=0) & (know11'=false); endmodule module provider2 = provider1 [y1=y2, st1=st2, dt1=dt2, tth1=tth2, trust11=trust21, know11=know21, alive1=alive2, alpha1=alpha2, trust21=trust11, know21=know11, // renaming parameters trust formula dt_init1=dt_init2, st_init1=st_init2, trust_init1=trust_init2, tth_init1=tth_init2, try11=try21, init_know11=init_know21, accept11=accept21, refuse11=refuse21, pay11=pay21, nopay11=nopay21, reduct1=reduct2, reveal11=reveal21, notreveal11=notreveal21, hide11=hide21] endmodule module provider3 = provider1 [y1=y3, st1=st3, dt1=dt3, tth1=tth3, trust11=trust31, know11=know31, alive1=alive3, alpha1=alpha3, trust31=trust11, know31=know11, // renaming parameters trust formula dt_init1=dt_init3, st_init1=st_init3, trust_init1=trust_init3, tth_init1=tth_init3,try11=try31, init_know11=init_know31, accept11=accept31, refuse11=refuse31, pay11=pay31, nopay11=nopay31, reduct1=reduct3, reveal11=reveal31, notreveal11=notreveal31, hide11=hide31] endmodule // trust level aliases const int level = 10; const int null = 0; const int low = 2; const int med = 5; const int high = 8; const int top = 10; // highest price in the market formula max_price = max((trust11 < tth1) ? cmin + ceil(((cmax - cmin) / tth1) * (tth1 - trust11)) : cmin, (trust21 < tth2) ? cmin + ceil(((cmax - cmin) / tth2) * (tth2 - trust21)) : cmin, (trust31 < tth3) ? cmin + ceil(((cmax - cmin) / tth3) * (tth3 - trust31)) : cmin); //formula max_price = cmax; // maximum difference between trust // changed to action reward formula max_diff = max(max(trust11-trust21,trust21-trust11), max(trust11-trust31,trust31-trust11), max(trust21-trust31,trust31-trust21)); // cost of obtaining services rewards "cost" !unpaid1 & y1=2 : (trust11 < tth1) ? cmin + ceil(((cmax - cmin) / tth1) * (tth1 - trust11)) : cmin; !unpaid1 & y2=2 : (trust21 < tth2) ? cmin + ceil(((cmax - cmin) / tth2) * (tth2 - trust21)) : cmin; !unpaid1 & y3=2 : (trust31 < tth3) ? cmin + ceil(((cmax - cmin) / tth3) * (tth3 - trust31)) : cmin; x1=41 : max_price; endrewards // obtain an paid service rewards "payed" !unpaid1 & y1=2 : 1; !unpaid1 & y2=2 : 1; !unpaid1 & y3=2 : 1; endrewards // obtain an unpaid service rewards "nopayed" unpaid1 & y1=2 : 1; unpaid1 & y2=2 : 1; unpaid1 & y3=2 : 1; endrewards // total services rewards "accepted" [accept11] true : 1; [accept21] true : 1; [accept31] true : 1; endrewards
We now extend the above model to a concurrent stochastic game model [KNPS18] by allowing the user to make requests and pay different service providers simultaneously and for the different providers to execute requests concurrently. There are 7 players: one for the user's interaction with each service provider, one for the user buying services directly and one for each of the 3 service providers.
// Trust models for user-centric networks based on the TSG in // M. Kwiatkowska, D. Parker and A. Simaitis // Strategic analysis of trust models for user-centric networks. // In: Proc. SR’13. EPTCS, vol. 112, pp. 53–60 (2013) // (have simplified the reward structures) // gxn/ghrs 25/03/18 // originally based on the trust model of // A. Bogliolo, P. Polidori, A. Aldini, W. Moreira, P. Mendes, M. Yildiz, C. Ballester, and J.-M. Seigneur. // Virtual Currency and Reputation-Based Cooperation Incentives in User-Centric Networks. // In: Proc. IWCMC-2012, Cyprus, 2012 // concurrent stochastic game csg const int K; // number of services const int td; // trust model // model parameters const double alpha_all = 0.8; // recommendation influence parameter const int st_init_all = med; // initial service trust for all providers const int reduct_all = td; // trust decrease for all providers const bool hide_all = false; // allow information hiding const double cancel = 0.05; // probability to cancel fair request const bool init_know_all = true; // sharing of initial trust const double die_prob = 0; // probability provider dies after serving a request const int cmax = 10; // maximum service cost const int cmin = 2; // minimum service cost player requesterm requester_m endplayer player requester1 requester1 endplayer player requester2 requester2 endplayer player requester3 requester3 endplayer player provider1 provider1 endplayer player provider2 provider2 endplayer player provider3 provider3 endplayer // probability to share information formula rev_prob = know21&(trust11>trust21) | know31&(trust11>trust31) ? 0 : 1; formula ps = ps1 + ps2 + ps3 + psm; // paid services formula nps = nps1 + nps2 + nps3; // not paid for services module requester_m xm : [0..2]; psm : [0..K]; // buy the service off-market [buym] xm=0 & ps+nps<K -> (xm'=1); [waitm] xm=0 & ps+nps<K -> true; // allow the requester to contact a different requester [paym] xm=1 -> (xm'=0) & (psm'=min(K,psm+1)); // finish [done] xm+x1+x2+x3=0 & y1+y2+y3=0 & ps+nps>=K -> (xm'=2); [done] xm=2 -> true; endmodule label "finished" = xm=2; // requester finished module requester1 x1 : [0..2] init 0; // states of the module //ns1 : [0..K] init 0; // number of requested services ps1 : [0..K] init 0; // number of payed services nps1 : [0..K] init 0; // number of unpayed services unpaid1 : bool init false; [try11] x1=0 & ps+nps<K & y1=0 -> (x1'=1) & (unpaid1'=false); [wait1] x1=0 & ps+nps<K -> true; // allow the user to contact a different provider [r1,accept11] x1=1 & y1=3 -> (x1'=2); [r1,refuse11] x1=1 & y1=4 -> (x1'=0); [pay11] x1=2 -> (x1'=0) & (ps1'=min(K,ps1+1)); [nopay11] x1=2 -> (x1'=0) & (nps1'=min(K,nps1+1)) & (unpaid1'=true); endmodule module requester2 = requester1[x1=x2,ps1=ps2,ps2=ps3,ps3=ps1,nps1=nps2,nps2=nps3,nps3=nps1,unpaid1=unpaid2,try11=try21,accept11=accept21,refuse11=refuse21,pay11=pay21,nopay11=nopay21,wait1=wait2,y1=y2,r1=r2] endmodule module requester3 = requester1[x1=x3,ps1=ps3,ps2=ps1,ps3=ps2,nps1=nps3,nps2=nps1,nps3=nps2,unpaid1=unpaid3,try11=try31,accept11=accept31,refuse11=refuse31,pay11=pay31,nopay11=nopay31,wait1=wait3,y1=y3,r1=r3] endmodule // factor alpha of the cost formula const double alpha1 = alpha_all; const double alpha2 = alpha_all; const double alpha3 = alpha_all; // trust formula formula trusteq1 = min(top, !know21 & !know31 ? trust11 : floor(alpha1*trust11 + (1-alpha1)*recommend)); formula recommend = ((know21 ? trust21 : 0) + (know31 ? trust31 : 0)) / ((know21 ? 1 : 0) + (know31 ? 1 : 0)); // initial knowledge parameters const bool init_know11 = init_know_all; const bool init_know21 = init_know_all; const bool init_know31 = init_know_all; // initial trust parameters const int dt_init1 = st_init_all; // dispositional trust const int st_init1 = st_init_all; // service trust level const int trust_init1 = dt_init1; // initial trust const int tth_init1 = high; // trust threshold (see the cost formula) const int dt_init2 = st_init_all; const int st_init2 = st_init_all; const int trust_init2 = dt_init2; const int tth_init2 = high; const int dt_init3 = st_init_all; const int st_init3 = st_init_all; const int trust_init3 = dt_init3; const int tth_init3 = high; // trust reduction rates (0:NULL; 1:-1; 2:-2) const int reduct1 = reduct_all; const int reduct2 = reduct_all; const int reduct3 = reduct_all; // enable information withholding // info about requester 1 const bool hide11 = hide_all; const bool hide21 = hide_all; const bool hide31 = hide_all; module provider1 alive1 : bool init true; y1 : [0..4] init 0; // states of the module st1 : [0..level] init st_init1; // service trust level dt1 : [0..level] init dt_init1; // dispositional trust tth1 : [0..level] init tth_init1; // trust threshold (see the cost formula) trust11 : [0..level] init trust_init1; // trust towards the requester know11 : bool init init_know11; // interaction flag // initiate connection with requester [p1,try11] alive1 & y1=0 & ps+nps<K -> ((trusteq1 < st1) ? 1 : 0) + ((trusteq1 < st1) ? 0 : 1) * cancel : (y1'=4) + (1-(((trusteq1 < st1) ? 1 : 0) + ((trusteq1 < st1) ? 0 : 1) * cancel)) : (y1'=3); [p1,try11] !alive1 & y1=0 & ps+nps<K -> (y1'=4); [p1,wait1] y1=0 & ps+nps<K -> true; // accept or refuse requester1 [accept11] y1=3 -> (y1'=1); [refuse11] y1=4 -> (y1'=0); // settle payment with requester1 [p1,pay11] (y1=1) -> (y1'=2) & (trust11' = (trust11 < top ? trust11+1 : top)); [p1,nopay11] (reduct1=1) & (y1=1) -> (y1'=2) & (trust11'=(trust11>null?trust11-1 : null)); [p1,nopay11] (reduct1=2) & (y1=1) -> (y1'=2) & (trust11'=(trust11>null?trust11-2 : null)); [p1,nopay11] (reduct1=0) & (y1=1) -> (y1'=2) & (trust11'=null); // decide to reveal info about requester to other providers or not [reveal11] (y1=2) -> (1-die_prob) * rev_prob : (y1'=0) & (know11'=true) + (1-die_prob) * (1-rev_prob) : (y1'=0) & (know11'=false) + die_prob : (y1'=0) & (alive1'=false) & (trust11'=trust_init1) & (know11'=false); [notreveal11] hide11 & (y1=2) -> (y1'=0) & (know11'=false); endmodule module provider2 = provider1 [y1=y2, st1=st2, dt1=dt2, tth1=tth2, trust11=trust21, know11=know21, alive1=alive2, alpha1=alpha2, trust21=trust11, know21=know11, dt_init1=dt_init2, st_init1=st_init2, trust_init1=trust_init2, tth_init1=tth_init2, try11=try21, init_know11=init_know21, accept11=accept21, refuse11=refuse21, p1=p2, pay11=pay21, nopay11=nopay21, reduct1=reduct2, reveal11=reveal21, notreveal11=notreveal21, hide11=hide21, wait1=wait2] endmodule module provider3 = provider1 [y1=y3, st1=st3, dt1=dt3, tth1=tth3, trust11=trust31, know11=know31, alive1=alive3, alpha1=alpha3, trust31=trust11, know31=know11, dt_init1=dt_init3, st_init1=st_init3, trust_init1=trust_init3, tth_init1=tth_init3, try11=try31, init_know11=init_know31, accept11=accept31, refuse11=refuse31, p1=p3, pay11=pay31, nopay11=nopay31, reduct1=reduct3, reveal11=reveal31, notreveal11=notreveal31, hide11=hide31, wait1=wait3] endmodule // trust level aliases const int level = 10; const int null = 0; const int low = 2; const int med = 5; const int high = 8; const int top = 10; // highest price in the market formula max_price = max((trust11 < tth1) ? cmin + ceil(((cmax - cmin) / tth1) * (tth1 - trust11)) : cmin, (trust21 < tth2) ? cmin + ceil(((cmax - cmin) / tth2) * (tth2 - trust21)) : cmin, (trust31 < tth3) ? cmin + ceil(((cmax - cmin) / tth3) * (tth3 - trust31)) : cmin); //formula max_price = cmax; // maximum difference between trust formula max_diff = max(max(trust11-trust21,trust21-trust11), max(trust11-trust31,trust31-trust11), max(trust21-trust31,trust31-trust21)); // cost of obtaining services rewards "cost" [pay11] true : (trust11+1 < tth1) ? cmin + ceil(((cmax - cmin) / tth1) * (tth1 - (trust11+1))) : cmin; [pay21] true : (trust21+1 < tth2) ? cmin + ceil(((cmax - cmin) / tth2) * (tth2 - (trust21+1))) : cmin; [pay31] true : (trust31+1 < tth3) ? cmin + ceil(((cmax - cmin) / tth3) * (tth3 - (trust31+1))) : cmin; [paym] true : max_price; endrewards // number of unpaid out of total rewards "nopayed" [done] xm+x1+x2+x3=0 & nps+ps=K : nps; endrewards // ratio of unpaid rewards "ratio" [done] xm+x1+x2+x3=0 & ps+nps=K : nps/K; endrewards
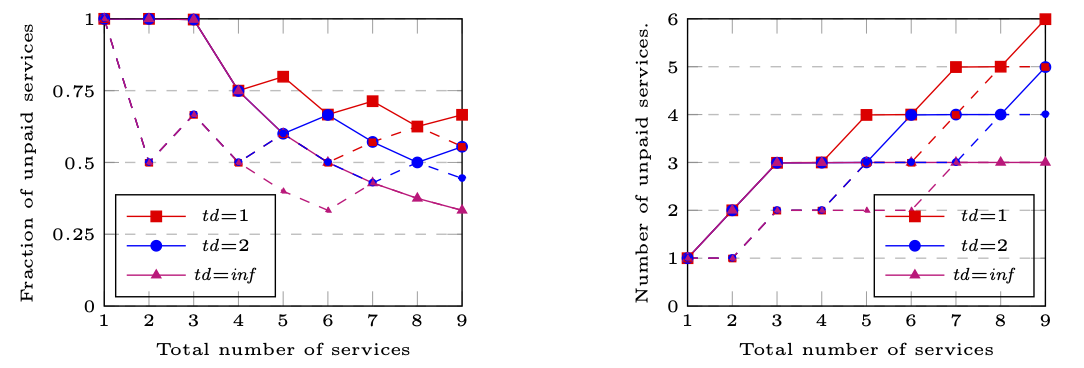
We consider both the maximum number and fraction of unpaid services that the user can ensure for each trust model for both models. Since the players for the models are different we need different properties to express these. For the turn-based model, we use the following formulae.
// expected number of unpaid <<requester1>> R{"nopayed"}max=? [ Fc "finished" ] // expected ration of unpaid <<requester1>> R{"nopayed"}max=? [ Fc "finished" ]/K
And for the concurrent stochastic game model:
// max expected number of unpaid services <<requesterm, requester1, requester2, requester3>> R{"nopayed"}max=? [Fc "finished"] // max expected fraction of unpaid services <<requesterm, requester1, requester2, requester3>> R{"ratio"}max=? [Fc "finished"]
The results are presented below using dashed lines for the TSG (SMG) model and solid lines for the CSG model. The results demonstrate that the user can take advantage of the fact that in the CSG model it can request multiple services at the same time, and obtain more services without paying before the different providers get a chance to inform each other about non-payment. In addition, the results show that having a more severe penalty on the trust measure for non-payment decreases the unpaid services the user can obtain.