(Qiu, Wu and Pedram)
This case study is based on a CTMC model of a 3 state Fujitsu disk drive taken from [QWP99]. As in [QWP99], we suppose that request inter-arrival distribution has the same (mean) expected value and equals 0.72, and that the maximum size of the service request queue (SRQ) is 20.
In this model the Service Provider (SP) has three states which are shown below.

The SP makes a transition from idle to busy whenever a request arrives for service. Similarly, it makes a transition from busy to idle whenever it finishes the service of a request. Transitions between sleep and idle are controlled by the PM. The only condition we impose on the PM is that, when the SRQ is full and the SP is in sleep, the PM switches the SP on, i.e. the SP moves to idle. The performance of the SP is given in the following tables where the data is taken from [QWP99]:
Average power consumption and service times of the SP
| sleep | idle | busy | average power | 0.13 | 0.95 | 2.15 | average service time | 0 | 0 | 0.008 |
Average energy consumption values for state transitions of the SP
| sleep | idle | busy | ||
| sleep | 0 | 7 | - | |
| idle | 0.067 | 0 | 0 | |
| busy | - | 0 | 0 |
Average transition times for state transitions of the SP
| sleep | idle | busy | ||
| sleep | 0 | 1.6 | - | |
| idle | 0.67 | 0 | 0 | |
| busy | - | 0 | 0 |
The module representing the SP is given below. Note that the actions corresponding to local changes of the SP synchronise with the PM, whereas the transitions corresponding to the service and arrival of requests synchronise with the SRQ.
// SERVICE PROVIDER // assume SP automatically // moves from idle to busy when ever a request arrives // moves from busy to idle when ever a request is served // rates of local state changes const double sleep2idle=10/16; const double idle2sleep=100/67; // rate of service const double service=1000/8; module SP sp : [0..2]; // 0 - sleep, 1 - idle, 2 - busy // SLEEP TO IDLE // when there is nothing in the queue go to idle [sleep2idle] sp=0 & q=0 -> sleep2idle : (sp'=1); // when there is something in the queue so start serving immediately [sleep2idle] sp=0 & q>0 -> sleep2idle : (sp'=2); // IDLE TO SLEEP [idle2sleep] sp=1 & q=0 -> idle2sleep : (sp'=0); // IDLE TO BUSY (when a request arrives) [request] sp=1 -> (sp'=2); [request] !sp=1 -> true; // need to add loop for other states // SERVE REQUESTS [serve] sp=2 & q>1 -> service : (sp'=2); [serve] sp=2 & q=1 -> service : (sp'=1); endmodule
Since there is only one queue, the SRQ and the SR can be combined into the following module:
// SERVICE REQUESTER AND SERVICE REQUEST QUEUE // size of queue const int QMAX=20; // rate of arrivals const double request=100/72; module SRQ q : [0..QMAX]; [request] true -> request : (q'=min(q+1,QMAX)); // request arrives [serve] q>0 -> (q'=q-1); // request served endmodule
Given a performance constraint (average number of requests awaiting service), we construct the optimal policy which minimises the average power consumption while satisfying the performance constraint. We obtained these policies by constructing the generator matrix of the system in PRISM and then, from this, constructing a linear optimization problem which we solve with Maple using its Simplex package.
Below, we list the policies obtained under a selection of different different performance constraints where, if no behaviour is specified, the choice of the policy is to do nothing (stay in the same state).
| Constraint | Policy | |
| average number of requests awaiting service <=20 |
when the SRQ is empty and the SP is in idle go to sleep | |
| average number of requests awaiting service <= 10 |
when the SRQ is full and the SP is in sleep go to idlewhen the SRQ is empty and the SP is in idle: go to sleep with probability 0.869135 stay in idle with probability 0.130865 | |
| average number of requests awaiting service <= 5 |
when the SRQ is full and the SP is in sleep go to idlewhen the SRQ is empty and the SP is in idle: go to sleep with probability 0.075140 stay in idle with probability 0.924860 | |
| average number of requests awaiting service <= 1 |
when the SRQ is full and the SP is in sleep go to idlewhen the SRQ is empty and the SP is in idle: go to sleep with probability 0.008963 stay in idle with probability 0.991037 | |
| average number of requests awaiting service <= 0.25 |
when the SRQ is full and the SP is in sleep go to idlewhen the SRQ is empty and the SP is in idle: go to sleep with probability 0.002014 stay in idle with probability 0.997986 | |
| average number of requests awaiting service <= 0.1 |
when the SRQ is full and the SP is in sleep go to idlewhen the SRQ is empty and the SP is in idle: go to sleep with probability 7.39e-04 stay in idle with probability 0.999261 |
It is then straightforward to define each policy in PRISM as a module. To illustrate this we give the module for the policy with performance constraint 1.
// POWER MANAGER performance constraint 1 // when the SRQ is full and the SP is in sleep go to idle // when the SRQ is empty and the SP is in idle: // go to sleep with probability 0.008963 and stay in idle with probability 0.991037 module PM p : [0..1]; // p=0 - loop or go sleep to idle // p=1 - idle to sleep // queue is full so go from sleep to idle [sleep2idle] q=QMAX -> (p'=p); // probabilistic choice when queue becomes empty [serve] q=1 -> 0.008963 : (p'=1); [serve] q=1 -> 0.991037 : (p'=0); [serve] q>1 -> true; // loops for remaining states [request] true -> (p'=0); // idle to sleep [idle2sleep] p=1 -> (p'=0); // reset p when queue is no longer empty endmodule
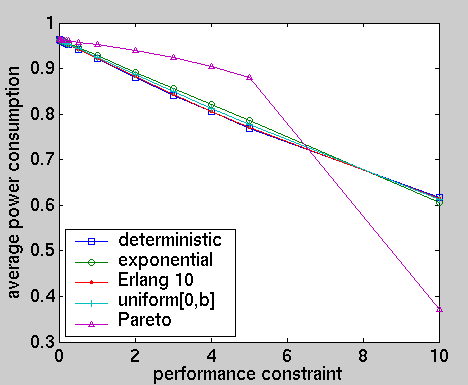
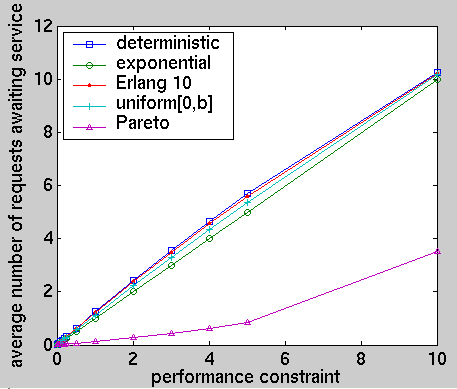
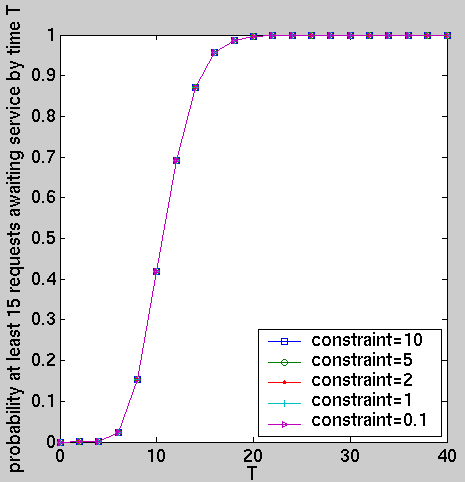
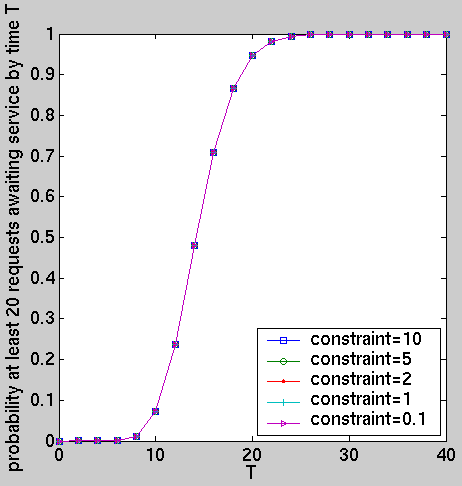
Using the results presented in [KNP02d], we have computed, for the optimal policies under different performance constraints and for a of selection distributions, with the same mean (0.72), modelling the inter-arrival time of requests:
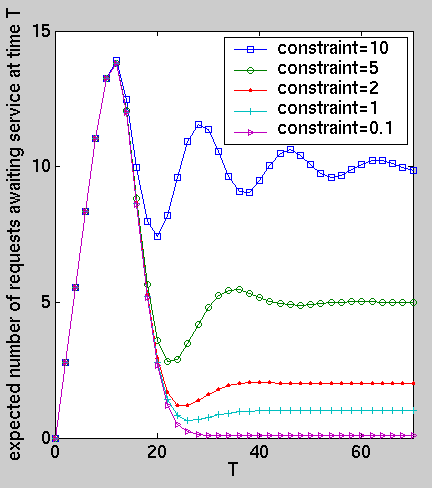
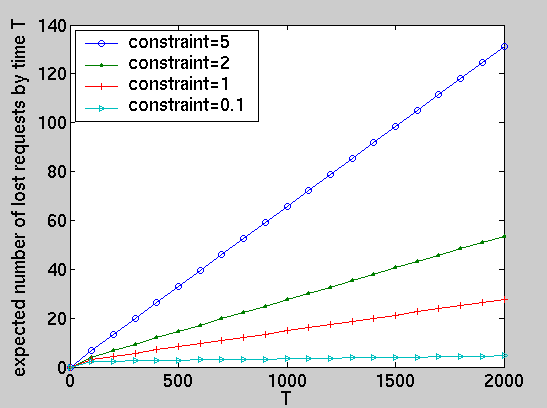
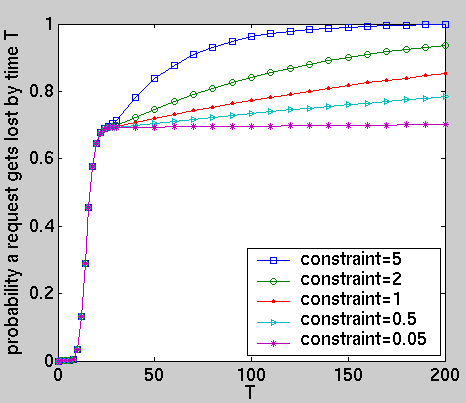
Furthermore, restricting the inter-arrival time to be exponentially distributed, we have computed the following performance measures for the optimal policies under different constraints: