(R. Brenguier)
Related publications: [KNPS19]
This case study is based on a model of power control in cellular networks from [Bre13]. In the model, phones emit signals over a cellular network and the signals can be strengthened by increasing the power level up to a bound. A stronger signal can improve transmission quality, but uses more energy and lowers the quality of other transmissions due to interference. We extend this model by adding a failure probability when a power level is increased and assume each phone has a limited battery capacity.
Based on [Bre13], we associate a reward structure with each phone representing transmission quality dependent both on its power level and that of other phones due to interference.
We assume there are two users, each with a single mobile phone. There are a number of parameters of the model:
There are two players in the CSG corresponding to the two users and each controls a single module. Each module contains a variable representing the current power level and current energy level of the corresponding phone. When a user's phone still has energy and the maximum power level has not been reached, the user can decide whether to try and increase the power level of not. As the two players have the same behaviour we use module renaming to define the module of the second user.
Each user has a reward structure representing the transmission quality of the phone, where the quality improves if the phone's power level is increased. However, the quality decreases as the other phone's power level is increased. If a phone has run out of energy, then the phone has no influence on the other phone's transmission quality.
// CSG model of power control in cellular networks // extends model of // Brenguier, R.: PRALINE: A tool for computing Nash equilibria in concurrent games. // In: Proc. CAV’13. LNCS, vol. 8044, pp. 890–895. Springer (2013) // now there is a probability increasing the power level fails // gxn/ghrs 24/07/2019 csg player user1 user1 endplayer player user2 user2 endplayer const int powmax; // power levels const int emax; // initial energy level const double fail; // probability fail to increment // model for first user/mobile module user1 e1 : [0..emax] init emax; pow1 : [1..powmax] init 1; // power1 // battery is empty [done1] e1=0 -> true; // battery no empty and do not increase battery level [n1] e1>0 -> (e1'=max(0,e1-pow1)); // battery not empty and increase battery level [inc1] e1>0 & (pow1<powmax) -> 1-fail : (pow1'=pow1+1) & (e1'=max(0,e1-pow1)) + fail : (e1'=max(0,e1-pow1)); endmodule // construct module of second user through renaming module user2=user1[e1=e2,pow1=pow2,n1=n2,inc1=inc2,done1=done2] endmodule // reward structures: ri for user i // their own power level has a positive influence // while the power level of other users is detrimental through interference rewards "r1" e1>0 & e2>0 : 1000*(1 - pow(2,-0.5*pow1 / (pow2 + 1))); e1>0 & e2=0 : 1000*(1 - pow(2,-0.5*pow1)); endrewards rewards "r2" e2>0 & e1>0 : 1000*(1 - pow(2,-0.5*pow2 / (pow1 + 1))); e2>0 & e1=0 : 1000*(1 - pow(2,-0.5*pow2)); endrewards
We consider non-zero sum properties where both users try and maximise their cumulative reward, both until their phone's battery is empty and over a fixed number of steps k. For this, we synthesise strategies that are social-welfare Nash equilibria (SWNE) [KNPS19].
const int k; // both users maximise the expected reward before their battery becomes empty <<user1:user2>>max=? (R{"r1"}[F e1=0] + R{"r2"}[F e2=0]) // both users maximise the expected reward for the first k steps <<user1:user2>>max=? (R{"r1"}[C<=k] + R{"r2"}[C<=k])
The following graph plots the values for players when they try to maximum their cumulative reward until their phone's battery is empty for emax=10 and fail=0.1 as powmax varies.
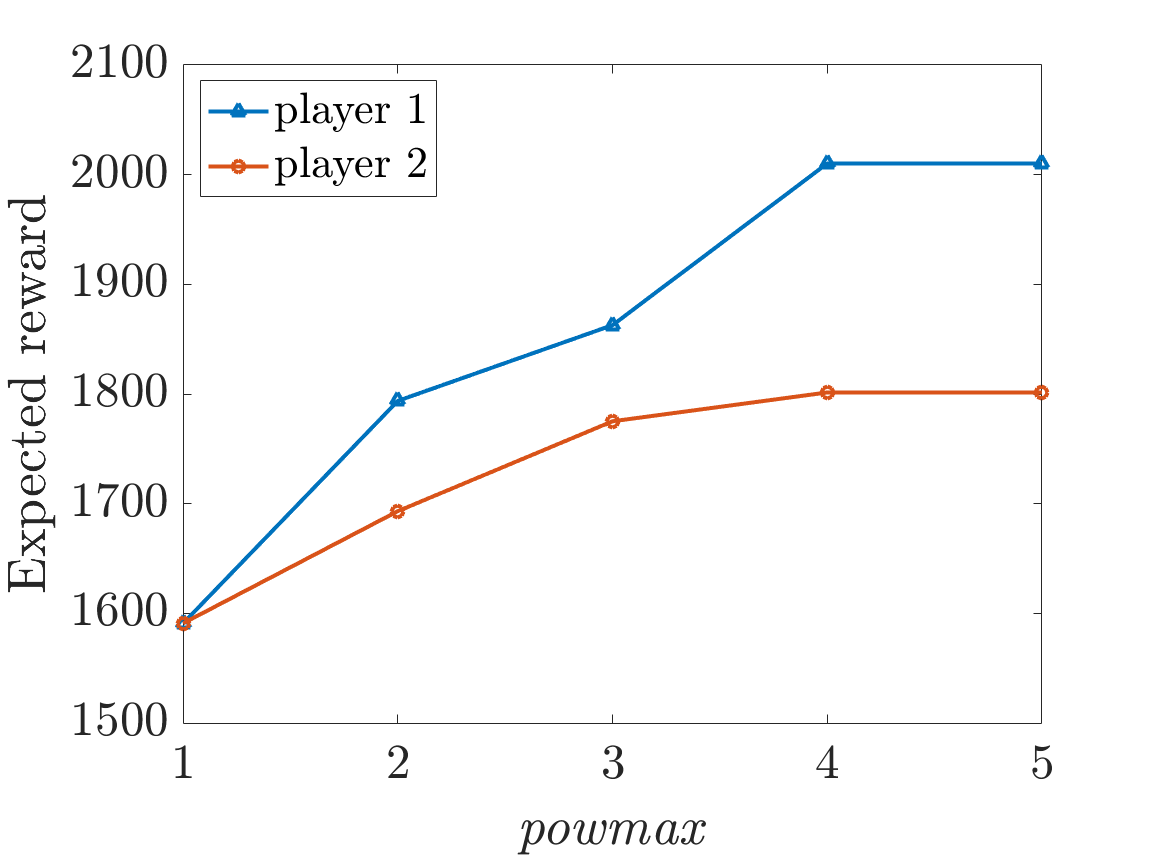
Synthesising the optimal strategies for the players we find that the values of the players are different because, if one increases their power level, this increases the overall reward (their reward increases, while the other’s decreases by a lesser amount due to interference) whereas, if both increase, the overall reward decreases (both rewards decrease due to interference).
For example the players' strategies in the case emax=10 and fail=0.1 for (first) powmax=2 and (second) powmax=3 are given below.
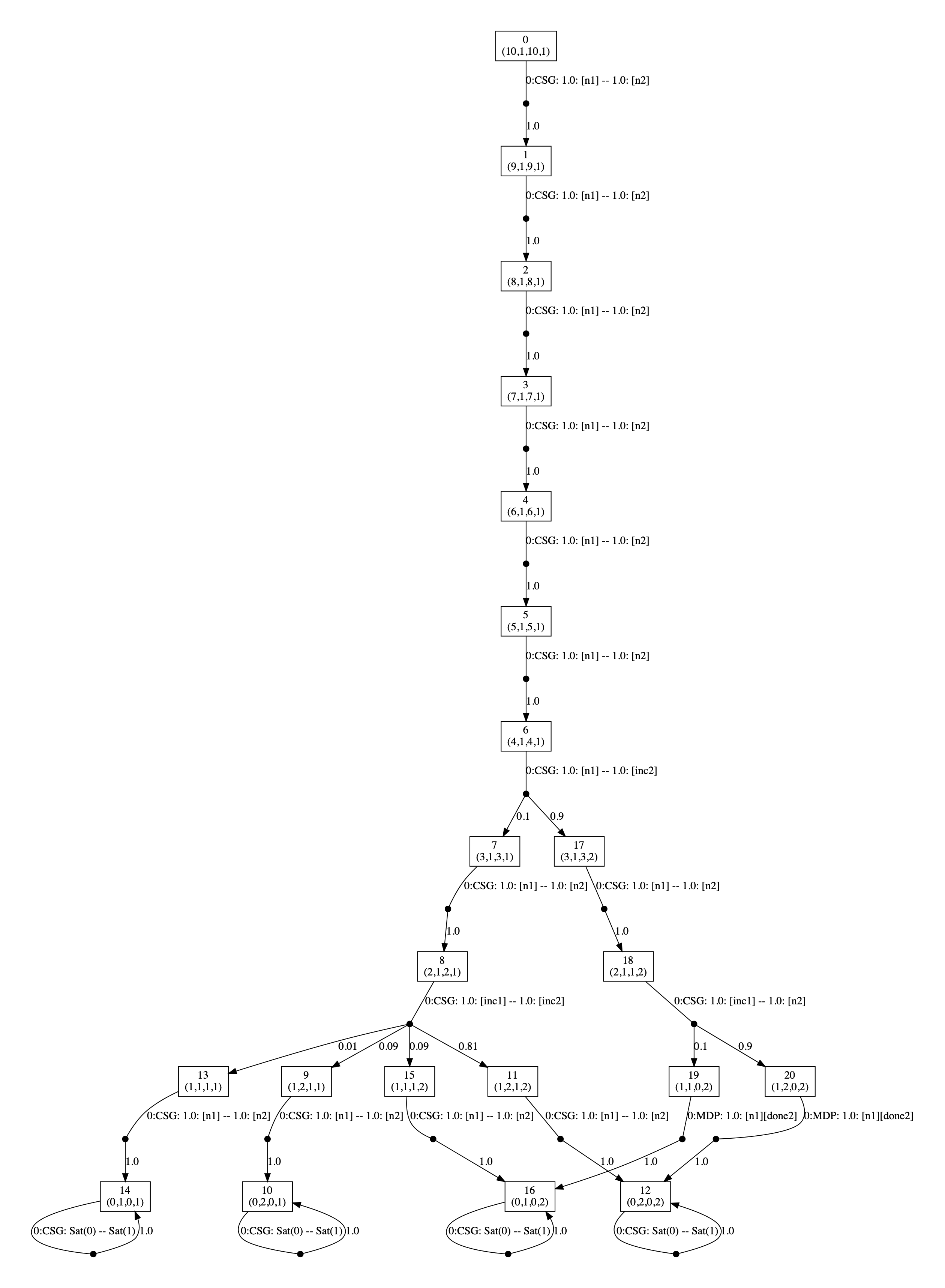
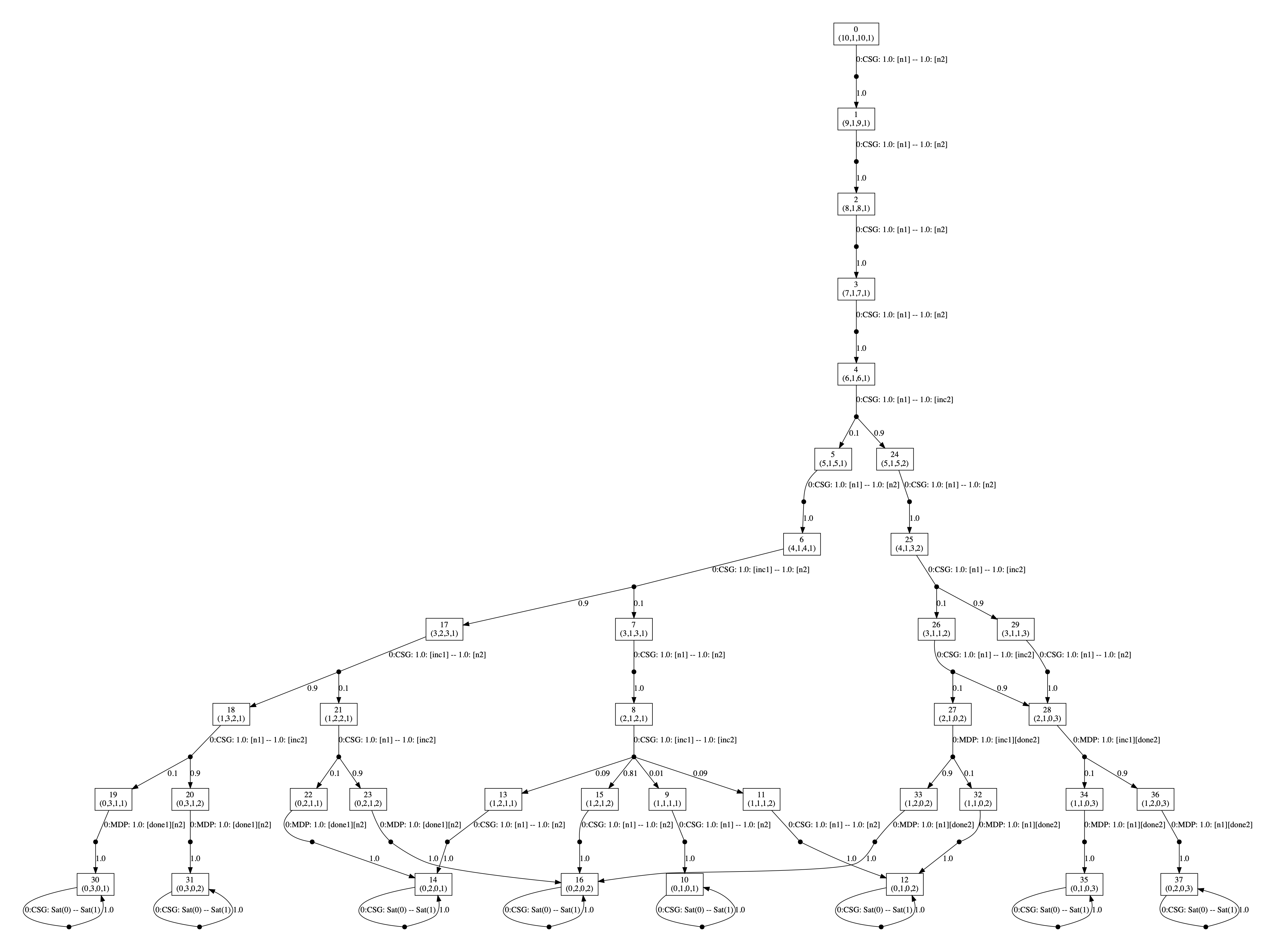
In the graph, the vertices correspond to the states of the game and are labelled with tuples corresponding to the values of the variables of the model: (e1,pow1,e2,pow2). The edges of the graph are labelled CSG followed by the choices for the two players (the probabilities of choosing available actions) with the choices for the different players separated by --. The first graph is generated by running the command:
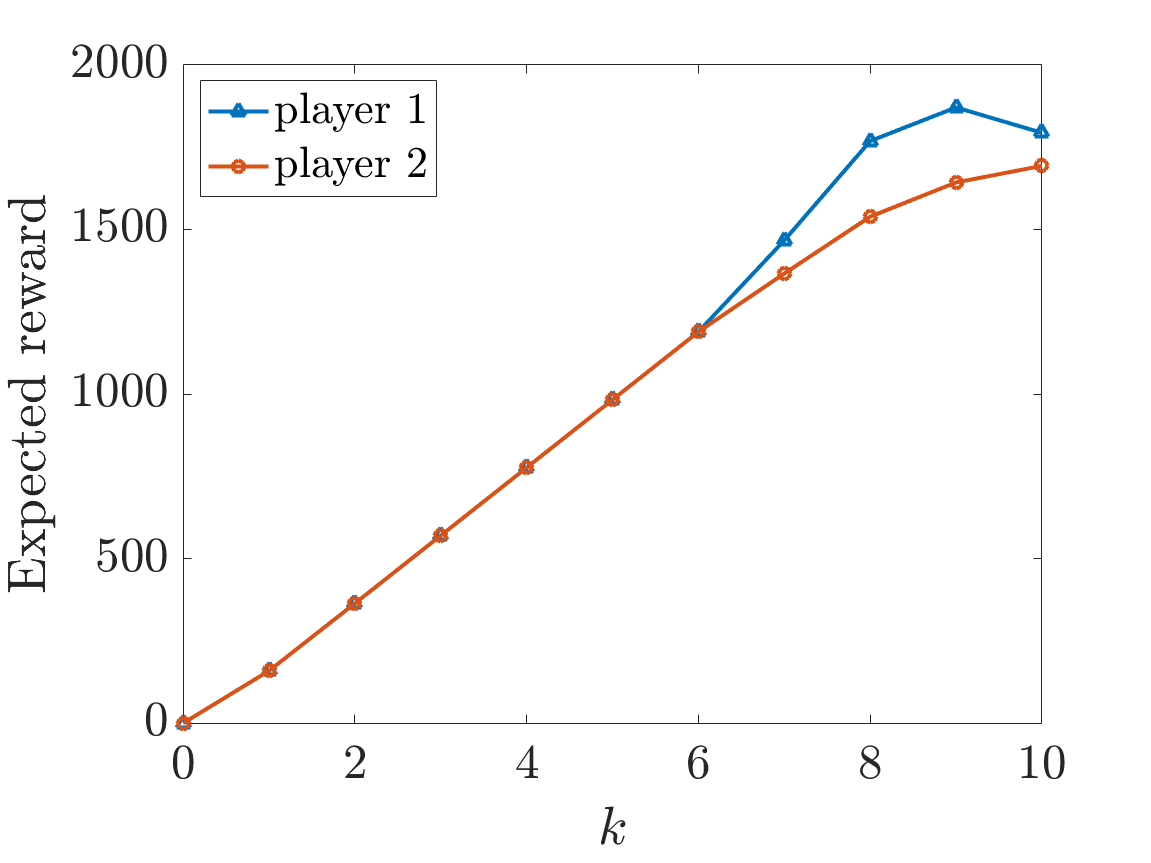
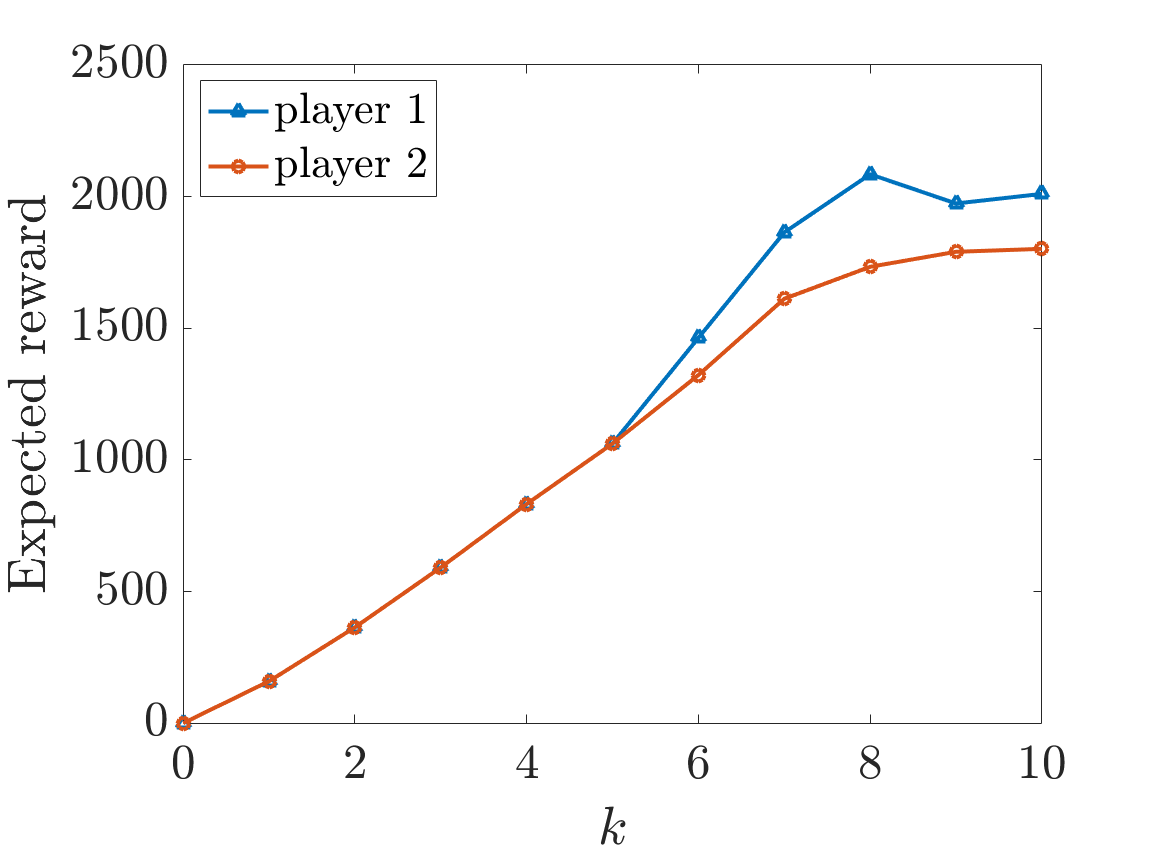
Now considering the second property, the graphs below plot the results for emax=10 and fail=0.1 as k varies. The first graph corresponds to when powmax=2 and the second graph when powmax=4.