(Q. Zhu, H. Li, Z. Han and T. Başar)
Related publications: [KNPS18]
A concurrent stochastic game (CSG) model for jamming multi-channel cognitive radio systems is presented in [ZLHB10]. The system consists of a number of channels which can be in either an occupied or idle state. The state of each channel remains fixed within a time slot and between slots is Markovian (i.e. the state changes randomly based only on the state of the channel in the previous slot). A secondary user has a subset of available channels and at each time-slot must decide which to use. There is a single attacker which again has a subset of available channels and at each time slot decides to send a jamming signal over one of them.
To model such systems, concurrency is required for the model to be meaningful, otherwise it is easy for the player whose turn follows the other player’s to 'win'. For example, if the jammer knows what channel is being deployed, then it can simply choose to jam that channel.
We assume there are four channels in total with the user being able to use the first three and the jammer being able to send a jamming signal over the last three.
We model each channel as a separate module. Since the behaviour of each channel is Markovian and not under the control of any player, the commands of the channel modules are unlabelled and not assigned to any player. Furthermore, since the behaviour of the channels is identical, we use module renaming of the first channel to define the second, third and fourth channels.
As well as the channel modules, there are two additional modules not under the control of any player. One keeps track of the current slot (there is an unspecified constant giving the maximum number of slots) and the other tracks the total number of sent messages. In this second module the behaviour is dependent on the choices of the user and the jammer as the state of the channel the user decides to send on. We therefore label the commands in this module by action lists for the user and the jammer and the update is dependent on the primed value of the state of the channel which the user decides to send on. Note we need only consider those action lists for which a message can be sent, e.g. we do not ned to consider any list for which channel the user sends on maches the channel that the jammer decides to send a jamming signal on.
The modules for the user and the jammer decide on what channel to send and jam respectively. The CSG also includes a reward structure which computes the number of messages sent.
// radio jamming CSG model taken from // A Stochastic Game Model for Jamming in Multi-Channel Cognitive Radio Systems // Quanyan Zhu, Husheng Li, Zhu Han and Tamer Basar // gxn 20/03/18 // user channels 1..3 // jamming channels 2..4 csg player user user endplayer player jammer jammer endplayer const int slots; // maximum time slots // probabilities that channels change state const double p01=0.75; // moves from free to busy const double p10=0.75; // moves from busy to free const double p00=1-p01; const double p11=1-p10; module time_slots // module to count the time slots t : [0..slots+1]; [] t<=slots -> (t'=t+1); endmodule module channel1 // module for channel 1 s1 : [0..1] init 1; // 0 - free and 1 in use (initially in use) [] t<slots & s1=0 -> p00 : (s1'=0) + p01 : (s1'=1); [] t<slots & s1=1 -> p10 : (s1'=0) + p11 : (s1'=1); endmodule // construct further channels with renaming module channel2 = channel1[s1=s2] endmodule module channel3 = channel1[s1=s3] endmodule module channel4 = channel1[s1=s4] endmodule module counter // module to count the number of messages sent correctly sent : [0..slots]; [send1,jam2] t<slots -> (sent'=min(slots,(s1'=0)?sent+1:sent)); [send1,jam3] t<slots -> (sent'=min(slots,(s1'=0)?sent+1:sent)); [send1,jam4] t<slots -> (sent'=min(slots,(s1'=0)?sent+1:sent)); [send2,jam3] t<slots -> (sent'=min(slots,(s2'=0)?sent+1:sent)); [send2,jam4] t<slots -> (sent'=min(slots,(s2'=0)?sent+1:sent)); [send3,jam2] t<slots -> (sent'=min(slots,(s3'=0)?sent+1:sent)); [send3,jam4] t<slots -> (sent'=min(slots,(s3'=0)?sent+1:sent)); endmodule module user // user [send1] t<slots -> true; [send2] t<slots -> true; [send3] t<slots -> true; endmodule module jammer // jammer module [jam2] t<slots -> true; [jam3] t<slots -> true; [jam4] t<slots -> true; endmodule rewards "rew" // reward for messages sent correctly t=slots : sent; endrewards
We consider both the maximum probability the user can ensure that at least half their messages are sent and the maximum expected number of messages the user can ensure are sent.
// maximum probability the user can ensure that at least half their messages are sent <<user>> Pmax=? [ F sent>=slots/2 ] // maximum expected number of messages the user can ensure are sent <<user>> R{"rew"}max=? [ F t=slots+1 ]
The following graphs plot the results for these properties as the number of slots varies.
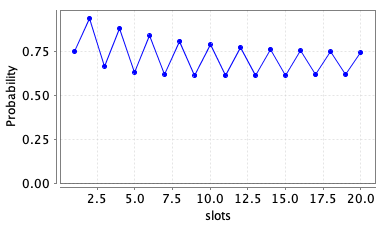
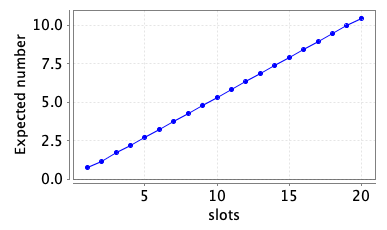
Performing strategy synthesis, we see that, if there are two slots, the optimal behaviour of the user is to initially send on channel 1 (as there is a high chance it will be free in the next slot and the jammer cannot jam this channel). In the next slot it again sends on channel 1, unless channel 1 was in use in the previous slot and both channels 2 and 3 were free and in this case it chooses between channels 2 and 3 uniformly at random. The reason is that in this case there is only a small chance channel 1 will be free when the message is sent and a high chance both that channel 2 and channel 3 will be free and the jammer cannot block both these channels while in all other cases there is either: