Related publications: [KNPS19, KNPS20]
This case study concerns three users trying to send packets using the slotted ALOHA protocol. In a time slot, if a single user tries to send a packet, there is a probability (q) that the packet is sent; as more users try and send, then the probability of success decreases. If sending a packet fails, the number of slots a user waits before resending is set according to an exponential backoff scheme. More precisely, each user maintains a backoff counter which it increases each time there is a failure (up to bmax) and, if the counter equals k, randomly chooses the slots to wait from {0,1,...,2k-1}.
The PRISM code representing a concurrent stochastic game of this scenario is given below. The model has three parameters: bcmax the maximum backoff counter, q the probability a packet is sent when two users try and send and D used for time-bounded properties. There are three players corresponding to the users trying to send packets.
The PRISM model also includes a reward structure corresponding to the time passage. Notice that time only passes when users are waiting before resending.
// model of aloha protocol with backoff scheme (three players) // each player tries to send a single message csg player usr1 user1 endplayer player usr2 user2 endplayer player usr3 user3 endplayer const int bcmax; // backoff limit const int M=pow(2,bcmax)-1; // backoff counter (slots to wait) // time can pass formula tick = (s1=0 | s1=2 | s1=3) & (s2=0 | s2=2 | s2=3) & (s3=0 | s3=2 | s3=3) & (tr1=0 & tr2=0 & tr3=0); const int D; // deadline // probability of successful transmission const double beta=1; const double q; formula n = tr1+tr2+tr3; formula rn = (n=3)? q/(pow(beta,2)*3) : (n=2)? q/(pow(beta,2)*2) : (n=1)? q : 0; module user1 s1 : [0..3] init 0; // local state tr1 : [0..1]; // try to transmit bc1 : [0..M]; // backoff counter cd1 : [0..bcmax]; // collision counter t1 : [0..2]; // can only wait for two time units before trying // wait or decide to try and transmit [wait1] tick & (s1=0 | s1=3) & t1<2 -> (t1'=t1+1); [trans1] tick & s1=0 -> (tr1'=1) & (t1'=0); // transmit [try1] tr1=1 -> (rn/n) : (s1'=3) & (tr1'=0) + (1-rn/n) : (s1'=1) & (tr1'=0) & (cd1'=min(bcmax,cd1+1)); // set backoff counter [sbc1] s1=1 & cd1=1 -> 1/2 : (s1'=2) & (bc1'=0) + 1/2 : (s1'=2) & (bc1'=1); [sbc1] s1=1 & cd1=2 -> 1/4 : (s1'=2) & (bc1'=0) + 1/4 : (s1'=2) & (bc1'=1) + 1/4 : (s1'=2) & (bc1'=2) + 1/4 : (s1'=2) & (bc1'=3); [sbc1] s1=1 & cd1=3 -> 1/8 : (s1'=2) & (bc1'=0) + 1/8 : (s1'=2) & (bc1'=1) + 1/8 : (s1'=2) & (bc1'=2) + 1/8 : (s1'=2) & (bc1'=3) + 1/8 : (s1'=2) & (bc1'=4) + 1/8 : (s1'=2) & (bc1'=5) + 1/8 : (s1'=2) & (bc1'=6) + 1/8 : (s1'=2) & (bc1'=7); [sbc1] s1=1 & cd1=4 -> 1/16 : (s1'=2) & (bc1'=0) + 1/16 : (s1'=2) & (bc1'=1) + 1/16 : (s1'=2) & (bc1'=2) + 1/16 : (s1'=2) & (bc1'=3) + 1/16 : (s1'=2) & (bc1'=4) + 1/16 : (s1'=2) & (bc1'=5) + 1/16 : (s1'=2) & (bc1'=6) + 1/16 : (s1'=2) & (bc1'=7) + 1/16 : (s1'=2) & (bc1'=8) + 1/16 : (s1'=2) & (bc1'=9) + 1/16 : (s1'=2) & (bc1'=10) + 1/16 : (s1'=2) & (bc1'=11) + 1/16 : (s1'=2) & (bc1'=12) + 1/16 : (s1'=2) & (bc1'=13) + 1/16 : (s1'=2) & (bc1'=14) + 1/16 : (s1'=2) & (bc1'=15); [sbc1] s1=1 & cd1=5 -> 1/32 : (s1'=2) & (bc1'=0) + 1/32 : (s1'=2) & (bc1'=1) + 1/32 : (s1'=2) & (bc1'=2) + 1/32 : (s1'=2) & (bc1'=3) + 1/32 : (s1'=2) & (bc1'=4) + 1/32 : (s1'=2) & (bc1'=5) + 1/32 : (s1'=2) & (bc1'=6) + 1/32 : (s1'=2) & (bc1'=7) + 1/32 : (s1'=2) & (bc1'=8) + 1/32 : (s1'=2) & (bc1'=9) + 1/32 : (s1'=2) & (bc1'=10) + 1/32 : (s1'=2) & (bc1'=11) + 1/32 : (s1'=2) & (bc1'=12) + 1/32 : (s1'=2) & (bc1'=13) + 1/32 : (s1'=2) & (bc1'=14) + 1/32 : (s1'=2) & (bc1'=15) + 1/32 : (s1'=2) & (bc1'=16) + 1/32 : (s1'=2) & (bc1'=17) + 1/32 : (s1'=2) & (bc1'=18) + 1/32 : (s1'=2) & (bc1'=19) + 1/32 : (s1'=2) & (bc1'=20) + 1/32 : (s1'=2) & (bc1'=21) + 1/32 : (s1'=2) & (bc1'=22) + 1/32 : (s1'=2) & (bc1'=23) + 1/32 : (s1'=2) & (bc1'=24) + 1/32 : (s1'=2) & (bc1'=25) + 1/32 : (s1'=2) & (bc1'=26) + 1/32 : (s1'=2) & (bc1'=27) + 1/32 : (s1'=2) & (bc1'=28) + 1/32 : (s1'=2) & (bc1'=29) + 1/32 : (s1'=2) & (bc1'=30) + 1/32 : (s1'=2) & (bc1'=31); [sbc1] s1=1 & cd1=6 -> 1/64 : (s1'=2) & (bc1'=0) + 1/64 : (s1'=2) & (bc1'=1) + 1/64 : (s1'=2) & (bc1'=2) + 1/64 : (s1'=2) & (bc1'=3) + 1/64 : (s1'=2) & (bc1'=4) + 1/64 : (s1'=2) & (bc1'=5) + 1/64 : (s1'=2) & (bc1'=6) + 1/64 : (s1'=2) & (bc1'=7) + 1/64 : (s1'=2) & (bc1'=8) + 1/64 : (s1'=2) & (bc1'=9) + 1/64 : (s1'=2) & (bc1'=10) + 1/64 : (s1'=2) & (bc1'=11) + 1/64 : (s1'=2) & (bc1'=12) + 1/64 : (s1'=2) & (bc1'=13) + 1/64 : (s1'=2) & (bc1'=14) + 1/64 : (s1'=2) & (bc1'=15) + 1/64 : (s1'=2) & (bc1'=16) + 1/64 : (s1'=2) & (bc1'=17) + 1/64 : (s1'=2) & (bc1'=18) + 1/64 : (s1'=2) & (bc1'=19) + 1/64 : (s1'=2) & (bc1'=20) + 1/64 : (s1'=2) & (bc1'=21) + 1/64 : (s1'=2) & (bc1'=22) + 1/64 : (s1'=2) & (bc1'=23) + 1/64 : (s1'=2) & (bc1'=24) + 1/64 : (s1'=2) & (bc1'=25) + 1/64 : (s1'=2) & (bc1'=26) + 1/64 : (s1'=2) & (bc1'=27) + 1/64 : (s1'=2) & (bc1'=28) + 1/64 : (s1'=2) & (bc1'=29) + 1/64 : (s1'=2) & (bc1'=30) + 1/64 : (s1'=2) & (bc1'=31) + 1/64 : (s1'=2) & (bc1'=32) + 1/64 : (s1'=2) & (bc1'=33) + 1/64 : (s1'=2) & (bc1'=34) + 1/64 : (s1'=2) & (bc1'=35) + 1/64 : (s1'=2) & (bc1'=36) + 1/64 : (s1'=2) & (bc1'=37) + 1/64 : (s1'=2) & (bc1'=38) + 1/64 : (s1'=2) & (bc1'=39) + 1/64 : (s1'=2) & (bc1'=40) + 1/64 : (s1'=2) & (bc1'=41) + 1/64 : (s1'=2) & (bc1'=42) + 1/64 : (s1'=2) & (bc1'=43) + 1/64 : (s1'=2) & (bc1'=44) + 1/64 : (s1'=2) & (bc1'=45) + 1/64 : (s1'=2) & (bc1'=46) + 1/64 : (s1'=2) & (bc1'=47) + 1/64 : (s1'=2) & (bc1'=48) + 1/64 : (s1'=2) & (bc1'=49) + 1/64 : (s1'=2) & (bc1'=50) + 1/64 : (s1'=2) & (bc1'=51) + 1/64 : (s1'=2) & (bc1'=52) + 1/64 : (s1'=2) & (bc1'=53) + 1/64 : (s1'=2) & (bc1'=54) + 1/64 : (s1'=2) & (bc1'=55) + 1/64 : (s1'=2) & (bc1'=56) + 1/64 : (s1'=2) & (bc1'=57) + 1/64 : (s1'=2) & (bc1'=58) + 1/64 : (s1'=2) & (bc1'=59) + 1/64 : (s1'=2) & (bc1'=60) + 1/64 : (s1'=2) & (bc1'=61) + 1/64 : (s1'=2) & (bc1'=62) + 1/64 : (s1'=2) & (bc1'=63); [sbc1] s1=1 & cd1=7 -> 1/128 : (s1'=2) & (bc1'=0) + 1/128 : (s1'=2) & (bc1'=1) + 1/128 : (s1'=2) & (bc1'=2) + 1/128 : (s1'=2) & (bc1'=3) + 1/128 : (s1'=2) & (bc1'=4) + 1/128 : (s1'=2) & (bc1'=5) + 1/128 : (s1'=2) & (bc1'=6) + 1/128 : (s1'=2) & (bc1'=7) + 1/128 : (s1'=2) & (bc1'=8) + 1/128 : (s1'=2) & (bc1'=9) + 1/128 : (s1'=2) & (bc1'=10) + 1/128 : (s1'=2) & (bc1'=11) + 1/128 : (s1'=2) & (bc1'=12) + 1/128 : (s1'=2) & (bc1'=13) + 1/128 : (s1'=2) & (bc1'=14) + 1/128 : (s1'=2) & (bc1'=15) + 1/128 : (s1'=2) & (bc1'=16) + 1/128 : (s1'=2) & (bc1'=17) + 1/128 : (s1'=2) & (bc1'=18) + 1/128 : (s1'=2) & (bc1'=19) + 1/128 : (s1'=2) & (bc1'=20) + 1/128 : (s1'=2) & (bc1'=21) + 1/128 : (s1'=2) & (bc1'=22) + 1/128 : (s1'=2) & (bc1'=23) + 1/128 : (s1'=2) & (bc1'=24) + 1/128 : (s1'=2) & (bc1'=25) + 1/128 : (s1'=2) & (bc1'=26) + 1/128 : (s1'=2) & (bc1'=27) + 1/128 : (s1'=2) & (bc1'=28) + 1/128 : (s1'=2) & (bc1'=29) + 1/128 : (s1'=2) & (bc1'=30) + 1/128 : (s1'=2) & (bc1'=31) + 1/128 : (s1'=2) & (bc1'=32) + 1/128 : (s1'=2) & (bc1'=33) + 1/128 : (s1'=2) & (bc1'=34) + 1/128 : (s1'=2) & (bc1'=35) + 1/128 : (s1'=2) & (bc1'=36) + 1/128 : (s1'=2) & (bc1'=37) + 1/128 : (s1'=2) & (bc1'=38) + 1/128 : (s1'=2) & (bc1'=39) + 1/128 : (s1'=2) & (bc1'=40) + 1/128 : (s1'=2) & (bc1'=41) + 1/128 : (s1'=2) & (bc1'=42) + 1/128 : (s1'=2) & (bc1'=43) + 1/128 : (s1'=2) & (bc1'=44) + 1/128 : (s1'=2) & (bc1'=45) + 1/128 : (s1'=2) & (bc1'=46) + 1/128 : (s1'=2) & (bc1'=47) + 1/128 : (s1'=2) & (bc1'=48) + 1/128 : (s1'=2) & (bc1'=49) + 1/128 : (s1'=2) & (bc1'=50) + 1/128 : (s1'=2) & (bc1'=51) + 1/128 : (s1'=2) & (bc1'=52) + 1/128 : (s1'=2) & (bc1'=53) + 1/128 : (s1'=2) & (bc1'=54) + 1/128 : (s1'=2) & (bc1'=55) + 1/128 : (s1'=2) & (bc1'=56) + 1/128 : (s1'=2) & (bc1'=57) + 1/128 : (s1'=2) & (bc1'=58) + 1/128 : (s1'=2) & (bc1'=59) + 1/128 : (s1'=2) & (bc1'=60) + 1/128 : (s1'=2) & (bc1'=61) + 1/128 : (s1'=2) & (bc1'=62) + 1/128 : (s1'=2) & (bc1'=63) + 1/128 : (s1'=2) & (bc1'=64) + 1/128 : (s1'=2) & (bc1'=65) + 1/128 : (s1'=2) & (bc1'=66) + 1/128 : (s1'=2) & (bc1'=67) + 1/128 : (s1'=2) & (bc1'=68) + 1/128 : (s1'=2) & (bc1'=69) + 1/128 : (s1'=2) & (bc1'=70) + 1/128 : (s1'=2) & (bc1'=71) + 1/128 : (s1'=2) & (bc1'=72) + 1/128 : (s1'=2) & (bc1'=73) + 1/128 : (s1'=2) & (bc1'=74) + 1/128 : (s1'=2) & (bc1'=75) + 1/128 : (s1'=2) & (bc1'=76) + 1/128 : (s1'=2) & (bc1'=77) + 1/128 : (s1'=2) & (bc1'=78) + 1/128 : (s1'=2) & (bc1'=79) + 1/128 : (s1'=2) & (bc1'=80) + 1/128 : (s1'=2) & (bc1'=81) + 1/128 : (s1'=2) & (bc1'=82) + 1/128 : (s1'=2) & (bc1'=83) + 1/128 : (s1'=2) & (bc1'=84) + 1/128 : (s1'=2) & (bc1'=85) + 1/128 : (s1'=2) & (bc1'=86) + 1/128 : (s1'=2) & (bc1'=87) + 1/128 : (s1'=2) & (bc1'=88) + 1/128 : (s1'=2) & (bc1'=89) + 1/128 : (s1'=2) & (bc1'=90) + 1/128 : (s1'=2) & (bc1'=91) + 1/128 : (s1'=2) & (bc1'=92) + 1/128 : (s1'=2) & (bc1'=93) + 1/128 : (s1'=2) & (bc1'=94) + 1/128 : (s1'=2) & (bc1'=95) + 1/128 : (s1'=2) & (bc1'=96) + 1/128 : (s1'=2) & (bc1'=97) + 1/128 : (s1'=2) & (bc1'=98) + 1/128 : (s1'=2) & (bc1'=99) + 1/128 : (s1'=2) & (bc1'=100) + 1/128 : (s1'=2) & (bc1'=101) + 1/128 : (s1'=2) & (bc1'=102) + 1/128 : (s1'=2) & (bc1'=103) + 1/128 : (s1'=2) & (bc1'=104) + 1/128 : (s1'=2) & (bc1'=105) + 1/128 : (s1'=2) & (bc1'=106) + 1/128 : (s1'=2) & (bc1'=107) + 1/128 : (s1'=2) & (bc1'=108) + 1/128 : (s1'=2) & (bc1'=109) + 1/128 : (s1'=2) & (bc1'=110) + 1/128 : (s1'=2) & (bc1'=111) + 1/128 : (s1'=2) & (bc1'=112) + 1/128 : (s1'=2) & (bc1'=113) + 1/128 : (s1'=2) & (bc1'=114) + 1/128 : (s1'=2) & (bc1'=115) + 1/128 : (s1'=2) & (bc1'=116) + 1/128 : (s1'=2) & (bc1'=117) + 1/128 : (s1'=2) & (bc1'=118) + 1/128 : (s1'=2) & (bc1'=119) + 1/128 : (s1'=2) & (bc1'=120) + 1/128 : (s1'=2) & (bc1'=121) + 1/128 : (s1'=2) & (bc1'=122) + 1/128 : (s1'=2) & (bc1'=123) + 1/128 : (s1'=2) & (bc1'=124) + 1/128 : (s1'=2) & (bc1'=125) + 1/128 : (s1'=2) & (bc1'=126) + 1/128 : (s1'=2) & (bc1'=127); [sbc1] s1=1 & cd1=8 -> 1/256 : (s1'=2) & (bc1'=0) + 1/256 : (s1'=2) & (bc1'=1) + 1/256 : (s1'=2) & (bc1'=2) + 1/256 : (s1'=2) & (bc1'=3) + 1/256 : (s1'=2) & (bc1'=4) + 1/256 : (s1'=2) & (bc1'=5) + 1/256 : (s1'=2) & (bc1'=6) + 1/256 : (s1'=2) & (bc1'=7) + 1/256 : (s1'=2) & (bc1'=8) + 1/256 : (s1'=2) & (bc1'=9) + 1/256 : (s1'=2) & (bc1'=10) + 1/256 : (s1'=2) & (bc1'=11) + 1/256 : (s1'=2) & (bc1'=12) + 1/256 : (s1'=2) & (bc1'=13) + 1/256 : (s1'=2) & (bc1'=14) + 1/256 : (s1'=2) & (bc1'=15) + 1/256 : (s1'=2) & (bc1'=16) + 1/256 : (s1'=2) & (bc1'=17) + 1/256 : (s1'=2) & (bc1'=18) + 1/256 : (s1'=2) & (bc1'=19) + 1/256 : (s1'=2) & (bc1'=20) + 1/256 : (s1'=2) & (bc1'=21) + 1/256 : (s1'=2) & (bc1'=22) + 1/256 : (s1'=2) & (bc1'=23) + 1/256 : (s1'=2) & (bc1'=24) + 1/256 : (s1'=2) & (bc1'=25) + 1/256 : (s1'=2) & (bc1'=26) + 1/256 : (s1'=2) & (bc1'=27) + 1/256 : (s1'=2) & (bc1'=28) + 1/256 : (s1'=2) & (bc1'=29) + 1/256 : (s1'=2) & (bc1'=30) + 1/256 : (s1'=2) & (bc1'=31) + 1/256 : (s1'=2) & (bc1'=32) + 1/256 : (s1'=2) & (bc1'=33) + 1/256 : (s1'=2) & (bc1'=34) + 1/256 : (s1'=2) & (bc1'=35) + 1/256 : (s1'=2) & (bc1'=36) + 1/256 : (s1'=2) & (bc1'=37) + 1/256 : (s1'=2) & (bc1'=38) + 1/256 : (s1'=2) & (bc1'=39) + 1/256 : (s1'=2) & (bc1'=40) + 1/256 : (s1'=2) & (bc1'=41) + 1/256 : (s1'=2) & (bc1'=42) + 1/256 : (s1'=2) & (bc1'=43) + 1/256 : (s1'=2) & (bc1'=44) + 1/256 : (s1'=2) & (bc1'=45) + 1/256 : (s1'=2) & (bc1'=46) + 1/256 : (s1'=2) & (bc1'=47) + 1/256 : (s1'=2) & (bc1'=48) + 1/256 : (s1'=2) & (bc1'=49) + 1/256 : (s1'=2) & (bc1'=50) + 1/256 : (s1'=2) & (bc1'=51) + 1/256 : (s1'=2) & (bc1'=52) + 1/256 : (s1'=2) & (bc1'=53) + 1/256 : (s1'=2) & (bc1'=54) + 1/256 : (s1'=2) & (bc1'=55) + 1/256 : (s1'=2) & (bc1'=56) + 1/256 : (s1'=2) & (bc1'=57) + 1/256 : (s1'=2) & (bc1'=58) + 1/256 : (s1'=2) & (bc1'=59) + 1/256 : (s1'=2) & (bc1'=60) + 1/256 : (s1'=2) & (bc1'=61) + 1/256 : (s1'=2) & (bc1'=62) + 1/256 : (s1'=2) & (bc1'=63) + 1/256 : (s1'=2) & (bc1'=64) + 1/256 : (s1'=2) & (bc1'=65) + 1/256 : (s1'=2) & (bc1'=66) + 1/256 : (s1'=2) & (bc1'=67) + 1/256 : (s1'=2) & (bc1'=68) + 1/256 : (s1'=2) & (bc1'=69) + 1/256 : (s1'=2) & (bc1'=70) + 1/256 : (s1'=2) & (bc1'=71) + 1/256 : (s1'=2) & (bc1'=72) + 1/256 : (s1'=2) & (bc1'=73) + 1/256 : (s1'=2) & (bc1'=74) + 1/256 : (s1'=2) & (bc1'=75) + 1/256 : (s1'=2) & (bc1'=76) + 1/256 : (s1'=2) & (bc1'=77) + 1/256 : (s1'=2) & (bc1'=78) + 1/256 : (s1'=2) & (bc1'=79) + 1/256 : (s1'=2) & (bc1'=80) + 1/256 : (s1'=2) & (bc1'=81) + 1/256 : (s1'=2) & (bc1'=82) + 1/256 : (s1'=2) & (bc1'=83) + 1/256 : (s1'=2) & (bc1'=84) + 1/256 : (s1'=2) & (bc1'=85) + 1/256 : (s1'=2) & (bc1'=86) + 1/256 : (s1'=2) & (bc1'=87) + 1/256 : (s1'=2) & (bc1'=88) + 1/256 : (s1'=2) & (bc1'=89) + 1/256 : (s1'=2) & (bc1'=90) + 1/256 : (s1'=2) & (bc1'=91) + 1/256 : (s1'=2) & (bc1'=92) + 1/256 : (s1'=2) & (bc1'=93) + 1/256 : (s1'=2) & (bc1'=94) + 1/256 : (s1'=2) & (bc1'=95) + 1/256 : (s1'=2) & (bc1'=96) + 1/256 : (s1'=2) & (bc1'=97) + 1/256 : (s1'=2) & (bc1'=98) + 1/256 : (s1'=2) & (bc1'=99) + 1/256 : (s1'=2) & (bc1'=100) + 1/256 : (s1'=2) & (bc1'=101) + 1/256 : (s1'=2) & (bc1'=102) + 1/256 : (s1'=2) & (bc1'=103) + 1/256 : (s1'=2) & (bc1'=104) + 1/256 : (s1'=2) & (bc1'=105) + 1/256 : (s1'=2) & (bc1'=106) + 1/256 : (s1'=2) & (bc1'=107) + 1/256 : (s1'=2) & (bc1'=108) + 1/256 : (s1'=2) & (bc1'=109) + 1/256 : (s1'=2) & (bc1'=110) + 1/256 : (s1'=2) & (bc1'=111) + 1/256 : (s1'=2) & (bc1'=112) + 1/256 : (s1'=2) & (bc1'=113) + 1/256 : (s1'=2) & (bc1'=114) + 1/256 : (s1'=2) & (bc1'=115) + 1/256 : (s1'=2) & (bc1'=116) + 1/256 : (s1'=2) & (bc1'=117) + 1/256 : (s1'=2) & (bc1'=118) + 1/256 : (s1'=2) & (bc1'=119) + 1/256 : (s1'=2) & (bc1'=120) + 1/256 : (s1'=2) & (bc1'=121) + 1/256 : (s1'=2) & (bc1'=122) + 1/256 : (s1'=2) & (bc1'=123) + 1/256 : (s1'=2) & (bc1'=124) + 1/256 : (s1'=2) & (bc1'=125) + 1/256 : (s1'=2) & (bc1'=126) + 1/256 : (s1'=2) & (bc1'=127) + 1/256 : (s1'=2) & (bc1'=128) + 1/256 : (s1'=2) & (bc1'=129) + 1/256 : (s1'=2) & (bc1'=130) + 1/256 : (s1'=2) & (bc1'=131) + 1/256 : (s1'=2) & (bc1'=132) + 1/256 : (s1'=2) & (bc1'=133) + 1/256 : (s1'=2) & (bc1'=134) + 1/256 : (s1'=2) & (bc1'=135) + 1/256 : (s1'=2) & (bc1'=136) + 1/256 : (s1'=2) & (bc1'=137) + 1/256 : (s1'=2) & (bc1'=138) + 1/256 : (s1'=2) & (bc1'=139) + 1/256 : (s1'=2) & (bc1'=140) + 1/256 : (s1'=2) & (bc1'=141) + 1/256 : (s1'=2) & (bc1'=142) + 1/256 : (s1'=2) & (bc1'=143) + 1/256 : (s1'=2) & (bc1'=144) + 1/256 : (s1'=2) & (bc1'=145) + 1/256 : (s1'=2) & (bc1'=146) + 1/256 : (s1'=2) & (bc1'=147) + 1/256 : (s1'=2) & (bc1'=148) + 1/256 : (s1'=2) & (bc1'=149) + 1/256 : (s1'=2) & (bc1'=150) + 1/256 : (s1'=2) & (bc1'=151) + 1/256 : (s1'=2) & (bc1'=152) + 1/256 : (s1'=2) & (bc1'=153) + 1/256 : (s1'=2) & (bc1'=154) + 1/256 : (s1'=2) & (bc1'=155) + 1/256 : (s1'=2) & (bc1'=156) + 1/256 : (s1'=2) & (bc1'=157) + 1/256 : (s1'=2) & (bc1'=158) + 1/256 : (s1'=2) & (bc1'=159) + 1/256 : (s1'=2) & (bc1'=160) + 1/256 : (s1'=2) & (bc1'=161) + 1/256 : (s1'=2) & (bc1'=162) + 1/256 : (s1'=2) & (bc1'=163) + 1/256 : (s1'=2) & (bc1'=164) + 1/256 : (s1'=2) & (bc1'=165) + 1/256 : (s1'=2) & (bc1'=166) + 1/256 : (s1'=2) & (bc1'=167) + 1/256 : (s1'=2) & (bc1'=168) + 1/256 : (s1'=2) & (bc1'=169) + 1/256 : (s1'=2) & (bc1'=170) + 1/256 : (s1'=2) & (bc1'=171) + 1/256 : (s1'=2) & (bc1'=172) + 1/256 : (s1'=2) & (bc1'=173) + 1/256 : (s1'=2) & (bc1'=174) + 1/256 : (s1'=2) & (bc1'=175) + 1/256 : (s1'=2) & (bc1'=176) + 1/256 : (s1'=2) & (bc1'=177) + 1/256 : (s1'=2) & (bc1'=178) + 1/256 : (s1'=2) & (bc1'=179) + 1/256 : (s1'=2) & (bc1'=180) + 1/256 : (s1'=2) & (bc1'=181) + 1/256 : (s1'=2) & (bc1'=182) + 1/256 : (s1'=2) & (bc1'=183) + 1/256 : (s1'=2) & (bc1'=184) + 1/256 : (s1'=2) & (bc1'=185) + 1/256 : (s1'=2) & (bc1'=186) + 1/256 : (s1'=2) & (bc1'=187) + 1/256 : (s1'=2) & (bc1'=188) + 1/256 : (s1'=2) & (bc1'=189) + 1/256 : (s1'=2) & (bc1'=190) + 1/256 : (s1'=2) & (bc1'=191) + 1/256 : (s1'=2) & (bc1'=192) + 1/256 : (s1'=2) & (bc1'=193) + 1/256 : (s1'=2) & (bc1'=194) + 1/256 : (s1'=2) & (bc1'=195) + 1/256 : (s1'=2) & (bc1'=196) + 1/256 : (s1'=2) & (bc1'=197) + 1/256 : (s1'=2) & (bc1'=198) + 1/256 : (s1'=2) & (bc1'=199) + 1/256 : (s1'=2) & (bc1'=200) + 1/256 : (s1'=2) & (bc1'=201) + 1/256 : (s1'=2) & (bc1'=202) + 1/256 : (s1'=2) & (bc1'=203) + 1/256 : (s1'=2) & (bc1'=204) + 1/256 : (s1'=2) & (bc1'=205) + 1/256 : (s1'=2) & (bc1'=206) + 1/256 : (s1'=2) & (bc1'=207) + 1/256 : (s1'=2) & (bc1'=208) + 1/256 : (s1'=2) & (bc1'=209) + 1/256 : (s1'=2) & (bc1'=210) + 1/256 : (s1'=2) & (bc1'=211) + 1/256 : (s1'=2) & (bc1'=212) + 1/256 : (s1'=2) & (bc1'=213) + 1/256 : (s1'=2) & (bc1'=214) + 1/256 : (s1'=2) & (bc1'=215) + 1/256 : (s1'=2) & (bc1'=216) + 1/256 : (s1'=2) & (bc1'=217) + 1/256 : (s1'=2) & (bc1'=218) + 1/256 : (s1'=2) & (bc1'=219) + 1/256 : (s1'=2) & (bc1'=220) + 1/256 : (s1'=2) & (bc1'=221) + 1/256 : (s1'=2) & (bc1'=222) + 1/256 : (s1'=2) & (bc1'=223) + 1/256 : (s1'=2) & (bc1'=224) + 1/256 : (s1'=2) & (bc1'=225) + 1/256 : (s1'=2) & (bc1'=226) + 1/256 : (s1'=2) & (bc1'=227) + 1/256 : (s1'=2) & (bc1'=228) + 1/256 : (s1'=2) & (bc1'=229) + 1/256 : (s1'=2) & (bc1'=230) + 1/256 : (s1'=2) & (bc1'=231) + 1/256 : (s1'=2) & (bc1'=232) + 1/256 : (s1'=2) & (bc1'=233) + 1/256 : (s1'=2) & (bc1'=234) + 1/256 : (s1'=2) & (bc1'=235) + 1/256 : (s1'=2) & (bc1'=236) + 1/256 : (s1'=2) & (bc1'=237) + 1/256 : (s1'=2) & (bc1'=238) + 1/256 : (s1'=2) & (bc1'=239) + 1/256 : (s1'=2) & (bc1'=240) + 1/256 : (s1'=2) & (bc1'=241) + 1/256 : (s1'=2) & (bc1'=242) + 1/256 : (s1'=2) & (bc1'=243) + 1/256 : (s1'=2) & (bc1'=244) + 1/256 : (s1'=2) & (bc1'=245) + 1/256 : (s1'=2) & (bc1'=246) + 1/256 : (s1'=2) & (bc1'=247) + 1/256 : (s1'=2) & (bc1'=248) + 1/256 : (s1'=2) & (bc1'=249) + 1/256 : (s1'=2) & (bc1'=250) + 1/256 : (s1'=2) & (bc1'=251) + 1/256 : (s1'=2) & (bc1'=252) + 1/256 : (s1'=2) & (bc1'=253) + 1/256 : (s1'=2) & (bc1'=254) + 1/256 : (s1'=2) & (bc1'=255); // backs off [boff1] tick & s1=2 & bc1>0 -> (bc1'=bc1-1); // decrement counter [boff1] tick & s1=2 & bc1=0 -> (tr1'=1) & (s1'=0); // finish backoff so transmit again endmodule // construct further users through renaming // (need to rename s2, s3, tr2 and tr3 as they appear in formulae) module user2=user1[s1=s2,s2=s1,tr1=tr2,tr2=tr1,bc1=bc2,cd1=cd2,wait1=wait2,trans1=trans2,try1=try2,boff1=boff2,sbc1=sbc2,t1=t2] endmodule module user3=user1[s1=s3,s3=s1,tr1=tr3,tr3=tr1,bc1=bc3,cd1=cd3,wait1=wait3,trans1=trans3,try1=try3,boff1=boff3,sbc1=sbc3,t1=t3] endmodule // module for counting when time passes (slots) module timer t : [0..D+1]; [] tick -> (t'=min(D+1,t+1)); endmodule // reward structure for time passage rewards "time" tick : 1; endrewards
We first consider zero-sum properties in which some of the users try to send their packets and the others try to prevent this from happening. We consider the following properties:
These properties are formally specified as follows for the case of three users, where the coalition is either just the first user or the second and third users.
// minimum expected time user 1 can guarantee to eventually send a packet <<usr1>>R{"time"}min=?[F s1=3] // minimum expected time users 2 and 3 can guarantee to eventually send their packets <<usr2,usr3>>R{"time"}min=?[F s2=3 & s3=3] // maximum probability user 1 can guarantee to send a packet within a deadline <<usr1>>Pmax=?[F (s1=3 & t<=D)] // maximum probability users 2 and 3 can guarantee to send their packets within a deadline <<usr2,usr3>>Pmax=?[F (s2=3 & s3=3 & t<=D)]
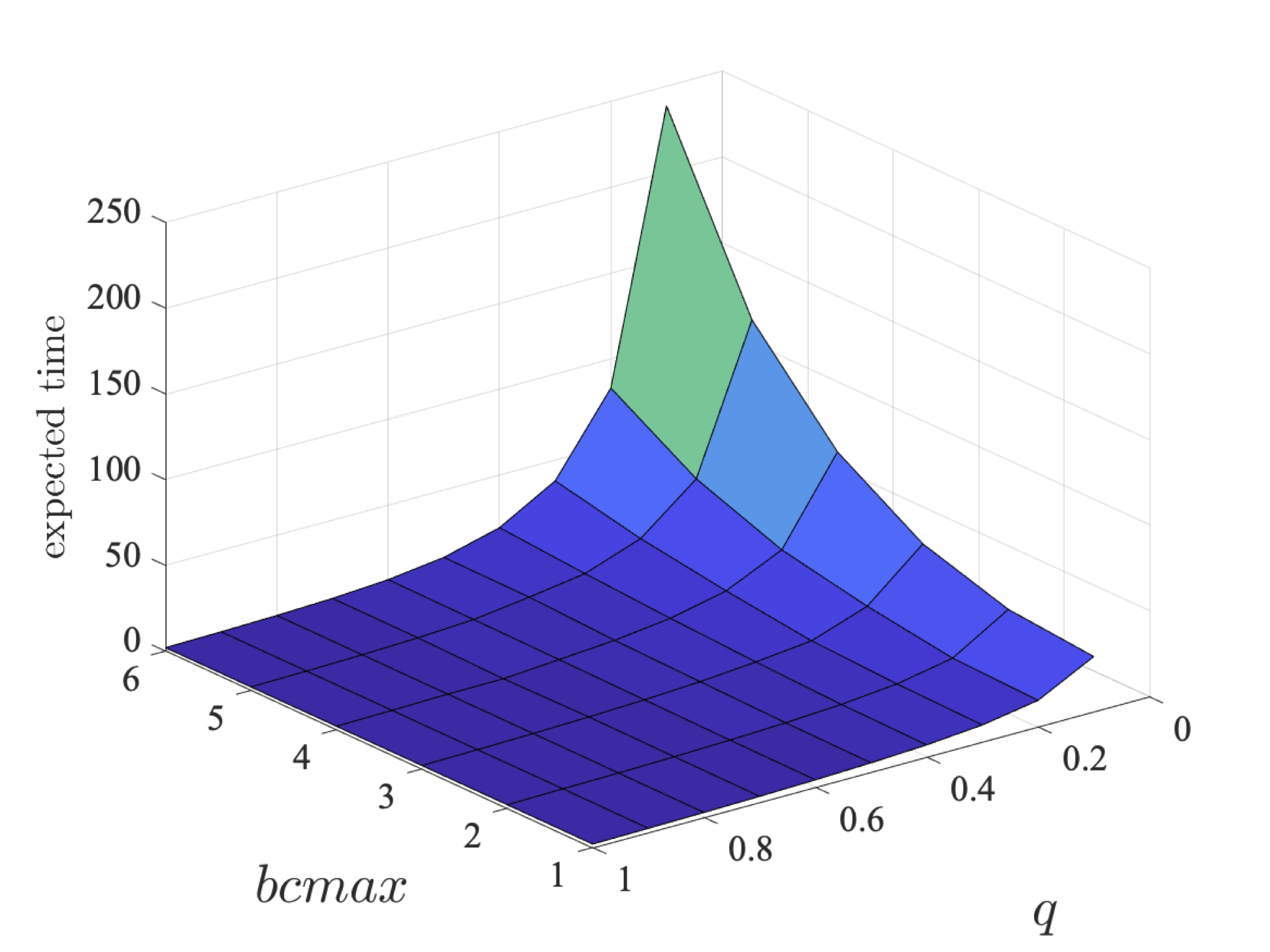
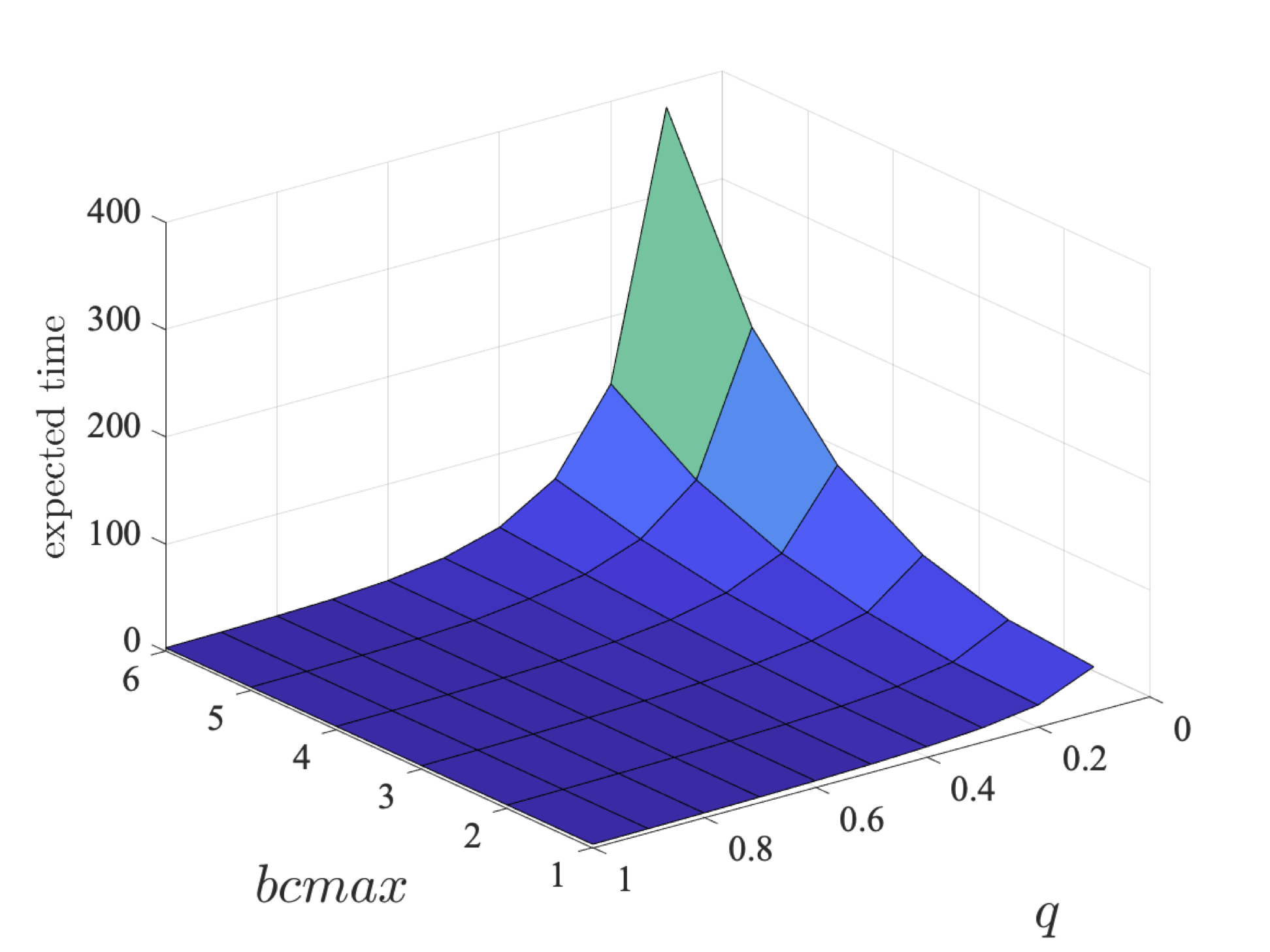
Considering the minimum expected time that a coalition can guarantee of eventually sending their packets, the following graphs plot the results for the coalition of only user 1 (left) and the coalition of users 2 and 3 (right) as q and bcmax vary.
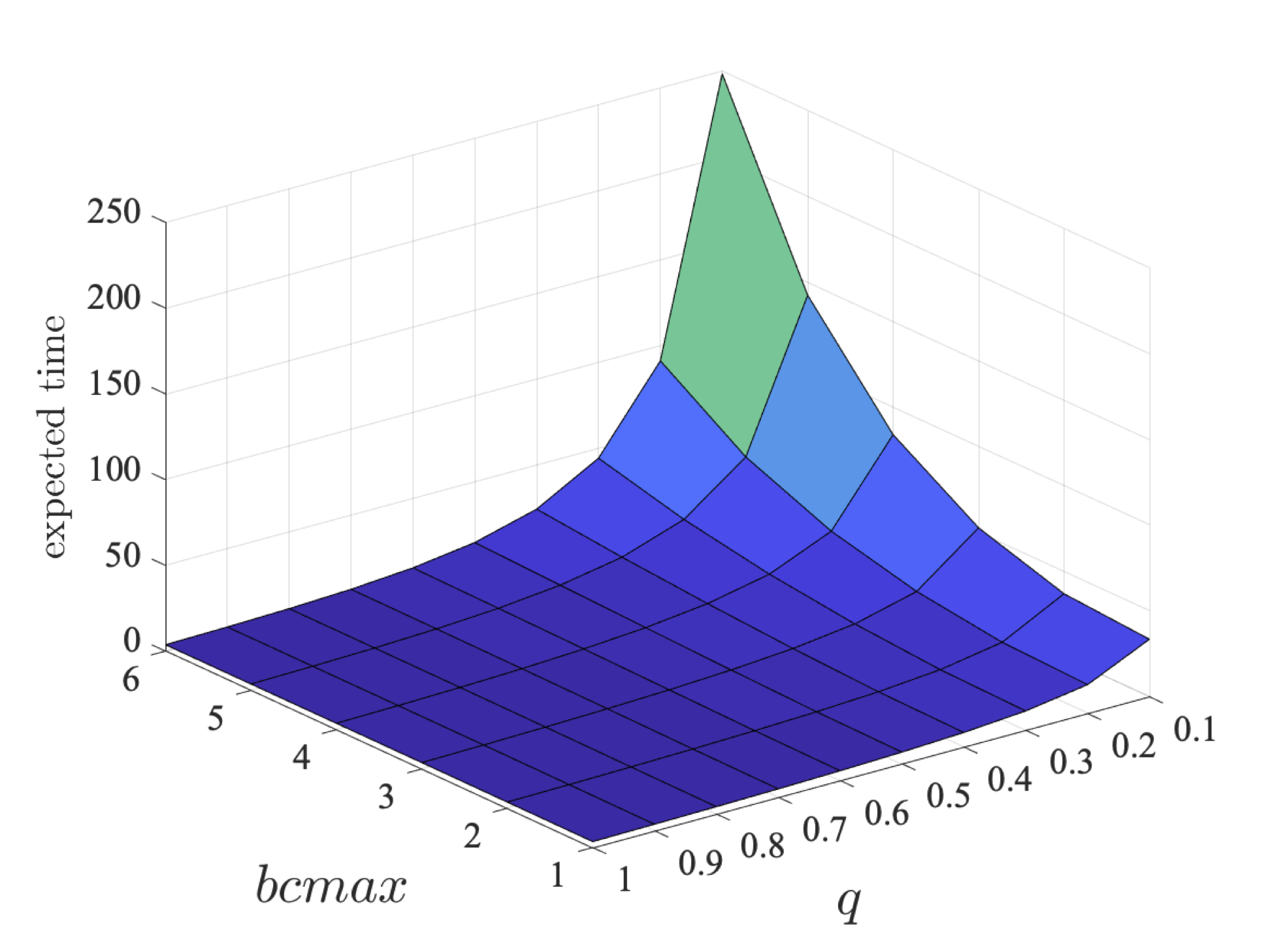
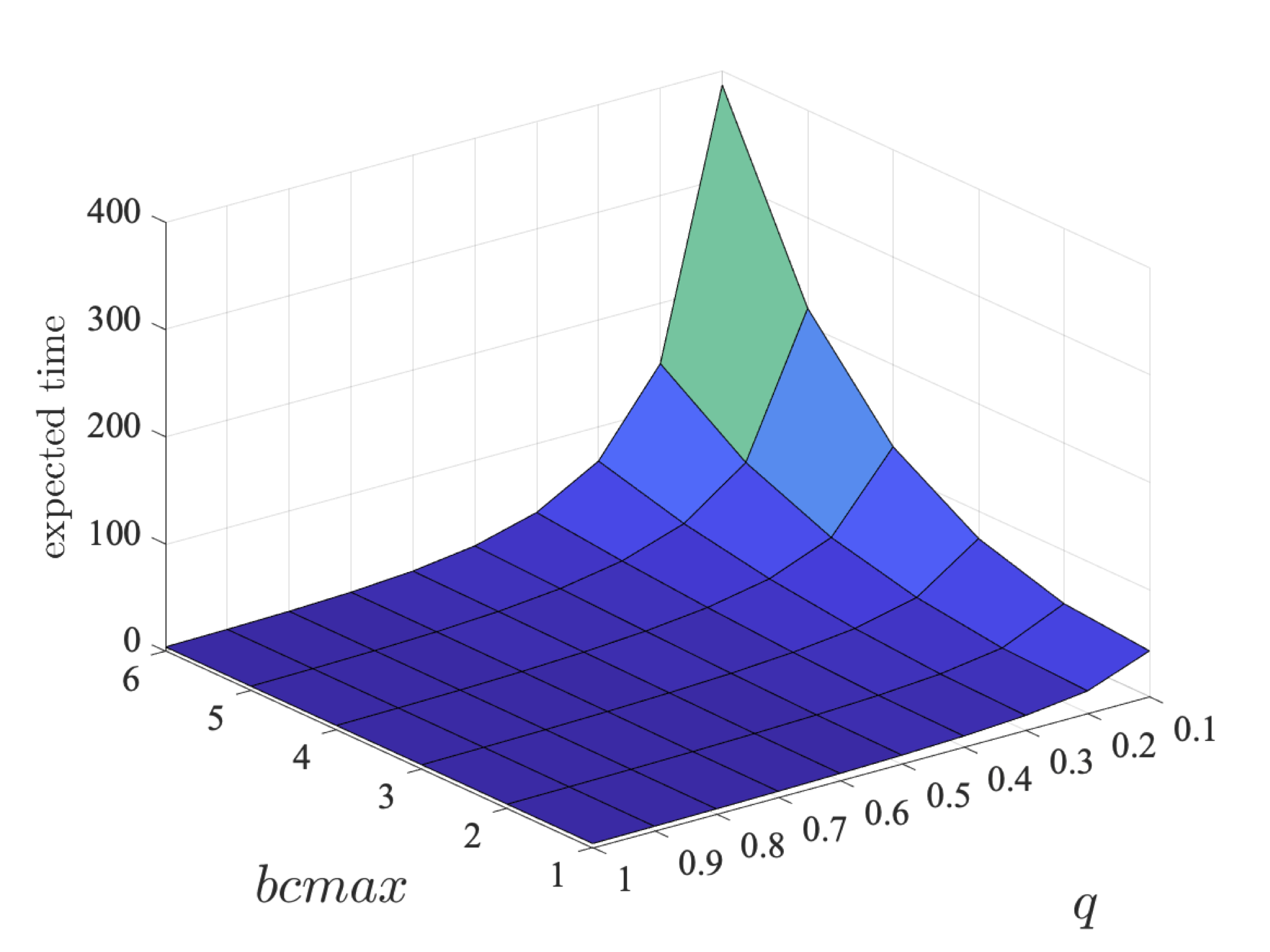
The results demonstrate that the expected time increases as the probability a packet is correctly sent decreases and the maximum value of the backoff counter increases. We also see that the expected time for the second coalition is larger, which is two be expected as this coalition consists of two users, rather than one, and therefore is the minimum expected time that can be guaranteed for two packets to be sent.
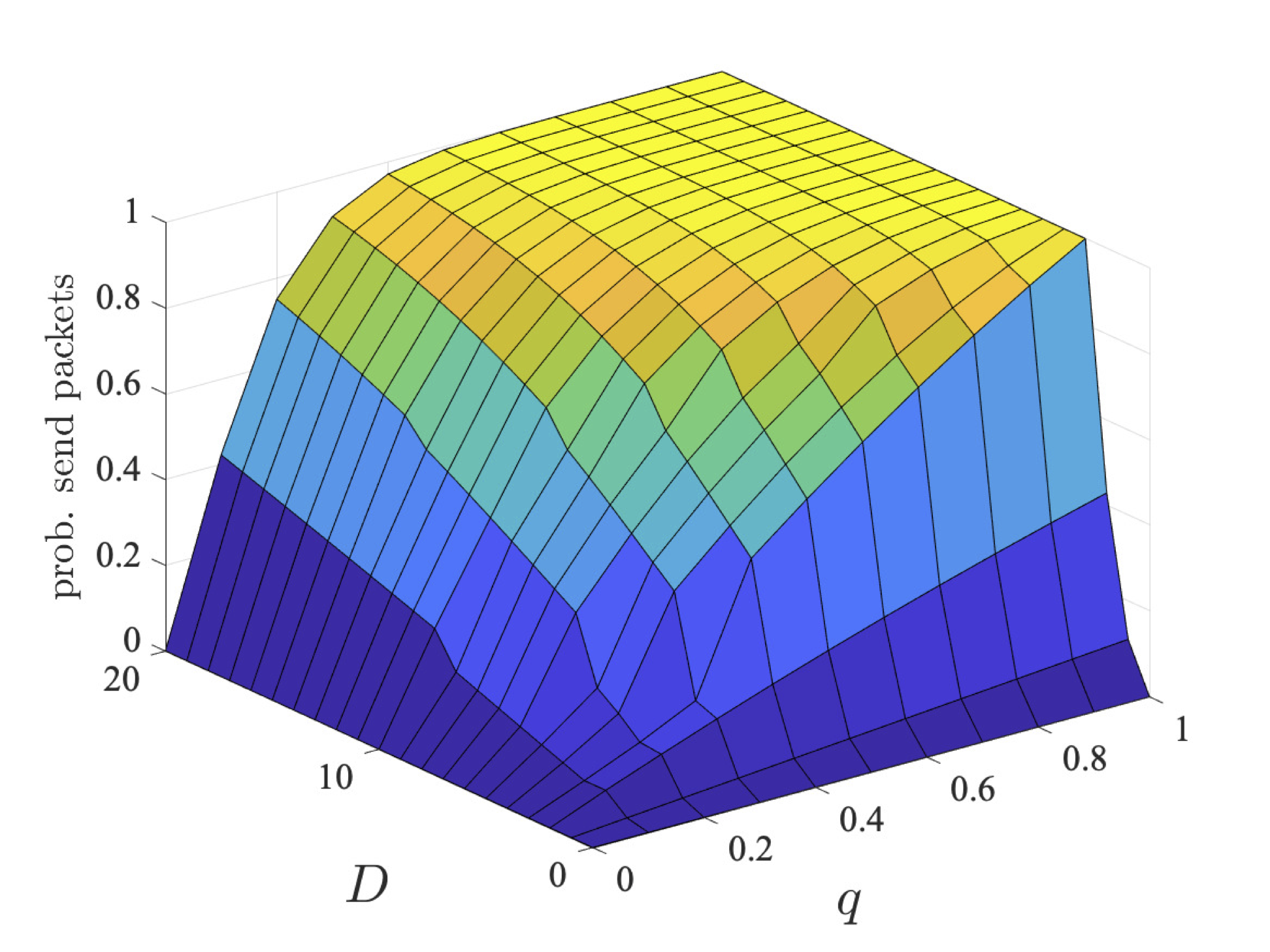
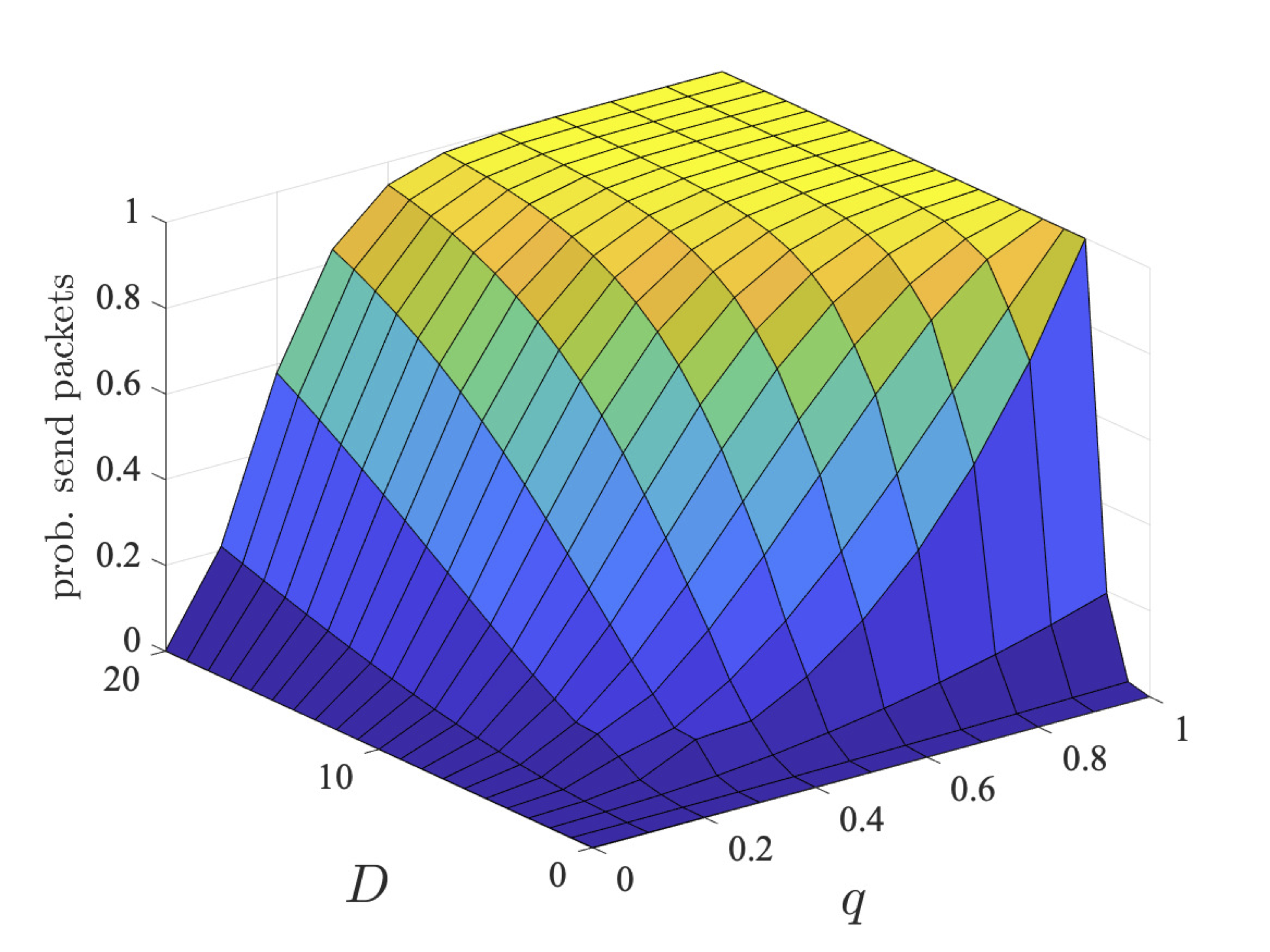
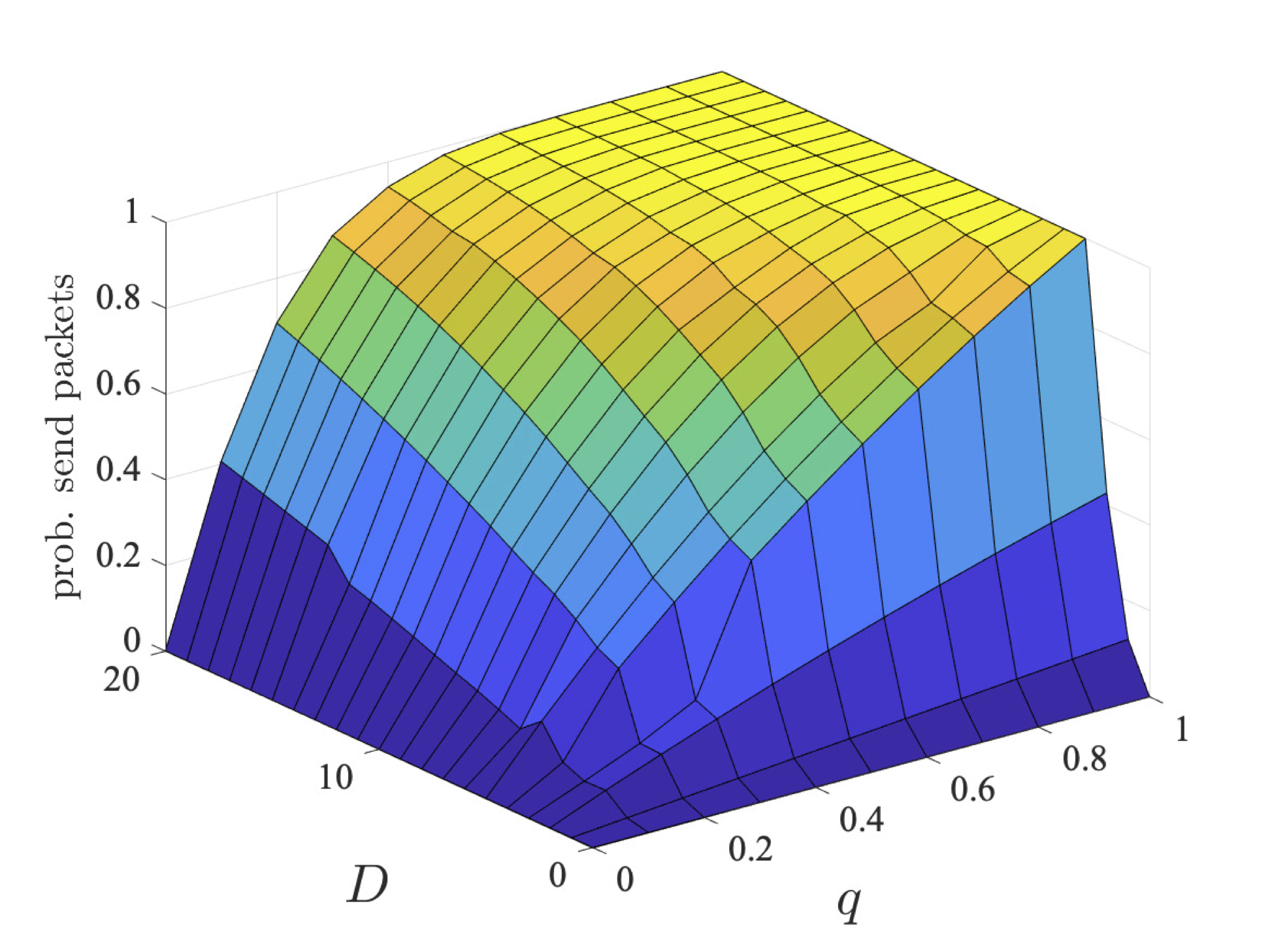
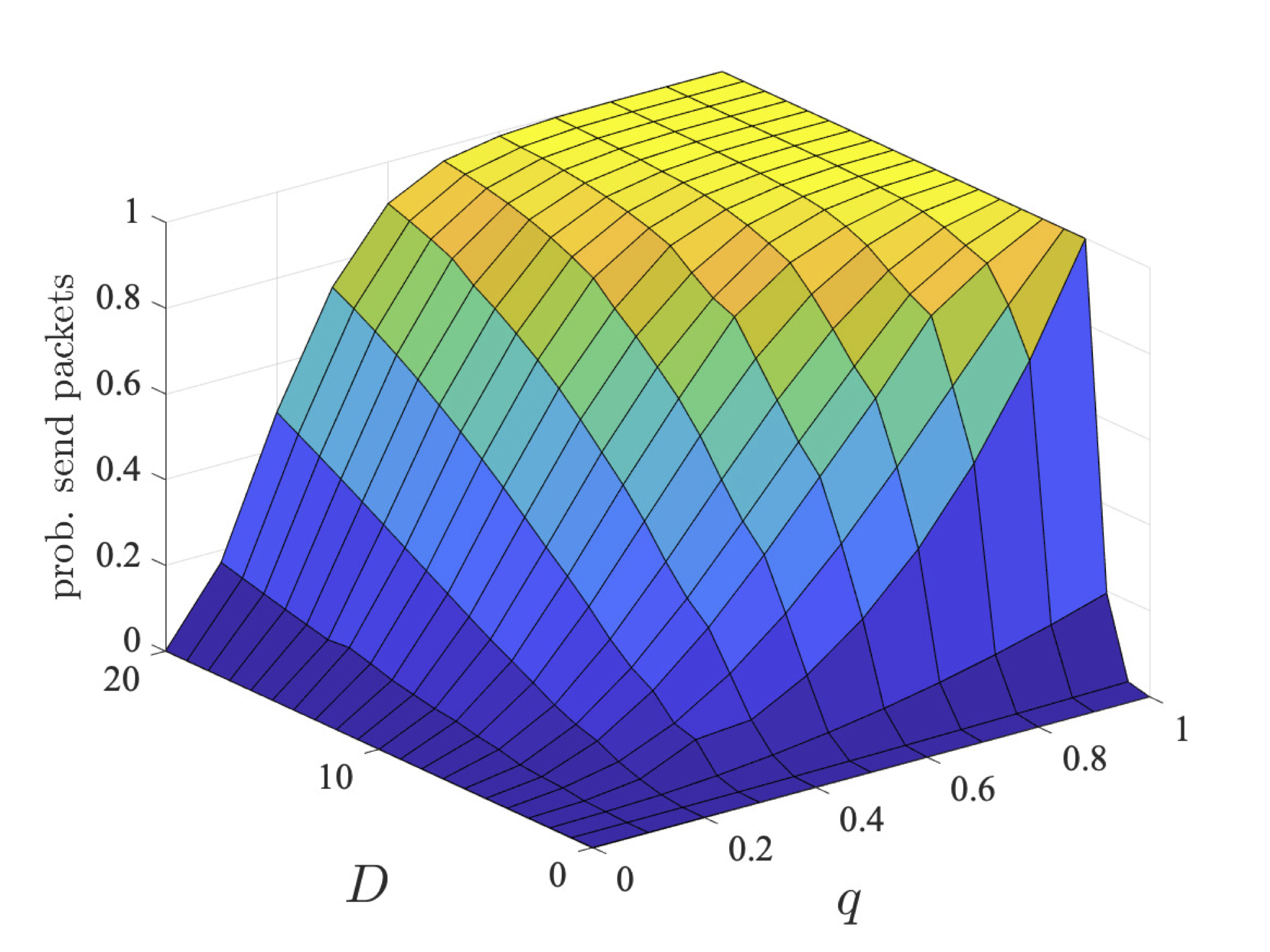
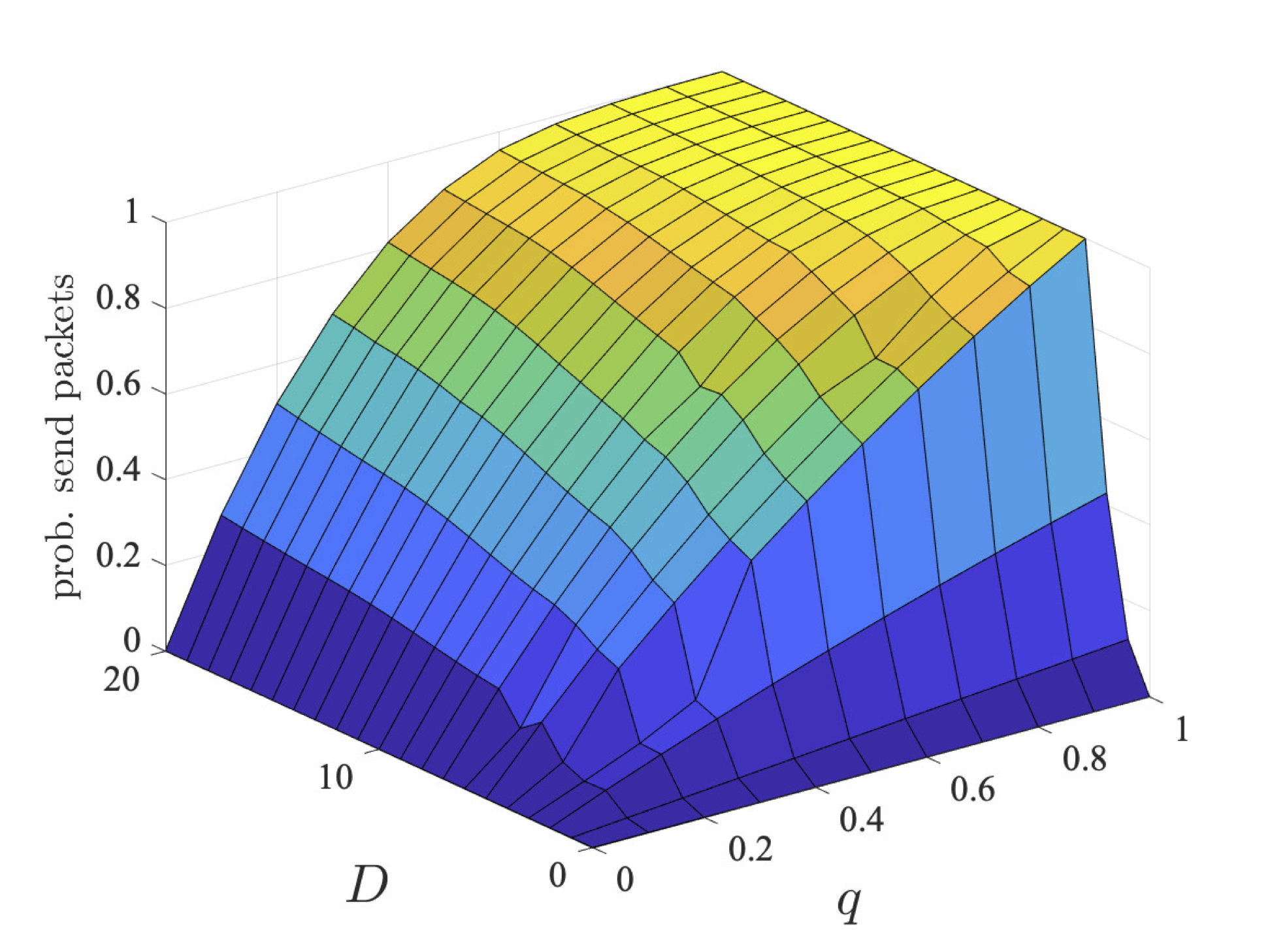
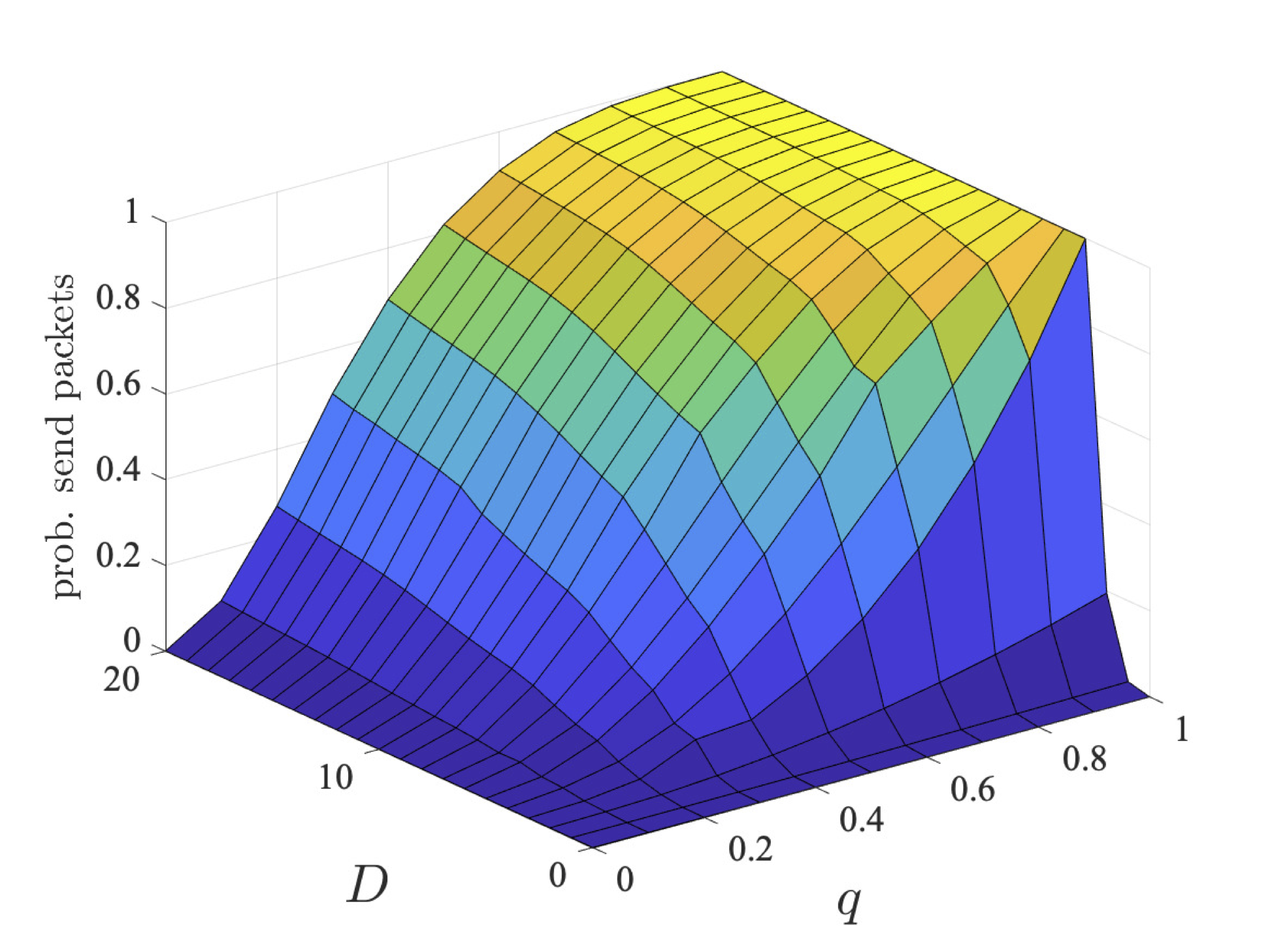
The graphs below plot the results for both the step-bounded property for the different coalitions of user 1 (left) and users 1 and 2 (right) as q and D vary for bcmax=1, 2 and 4.
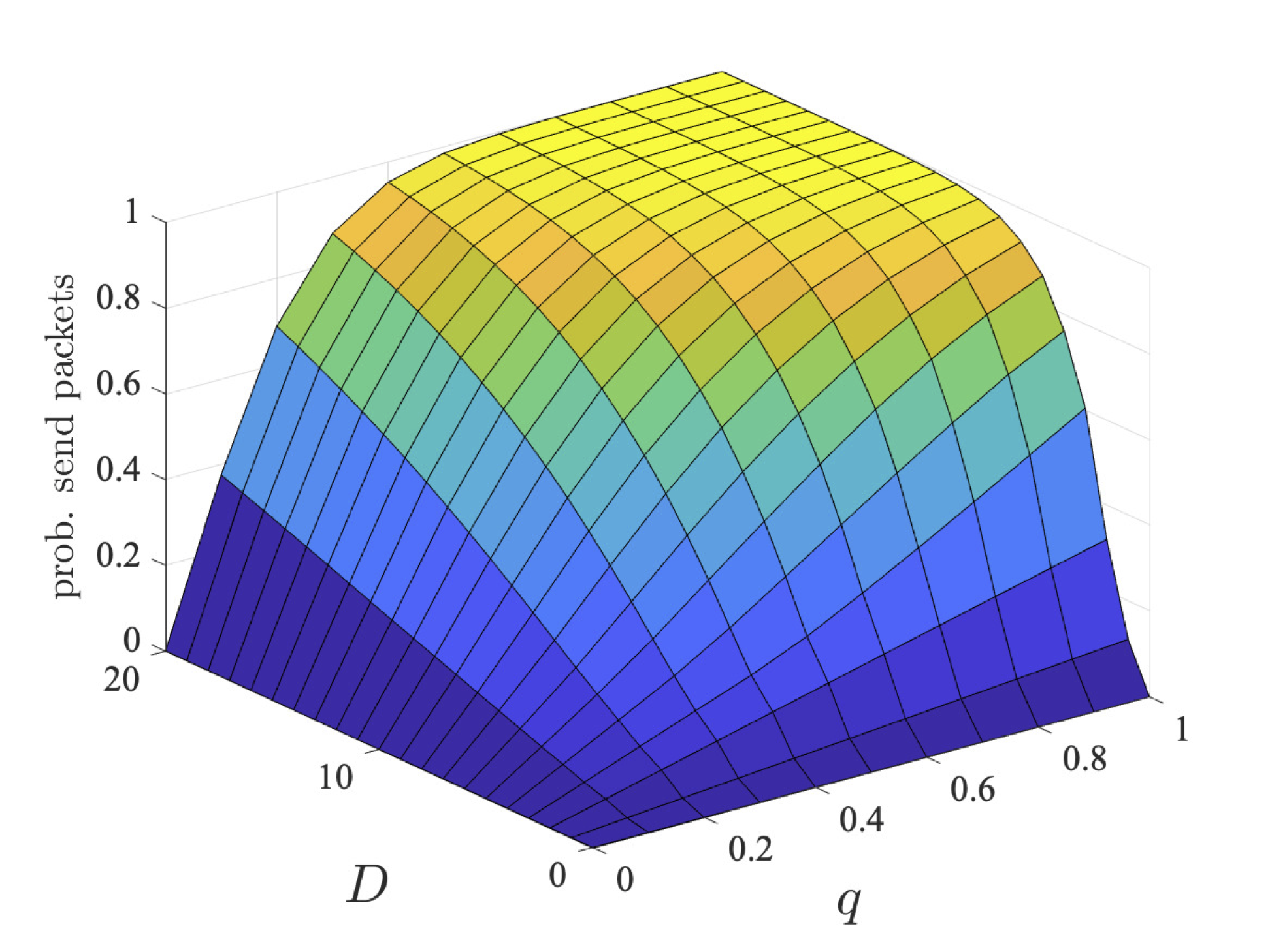
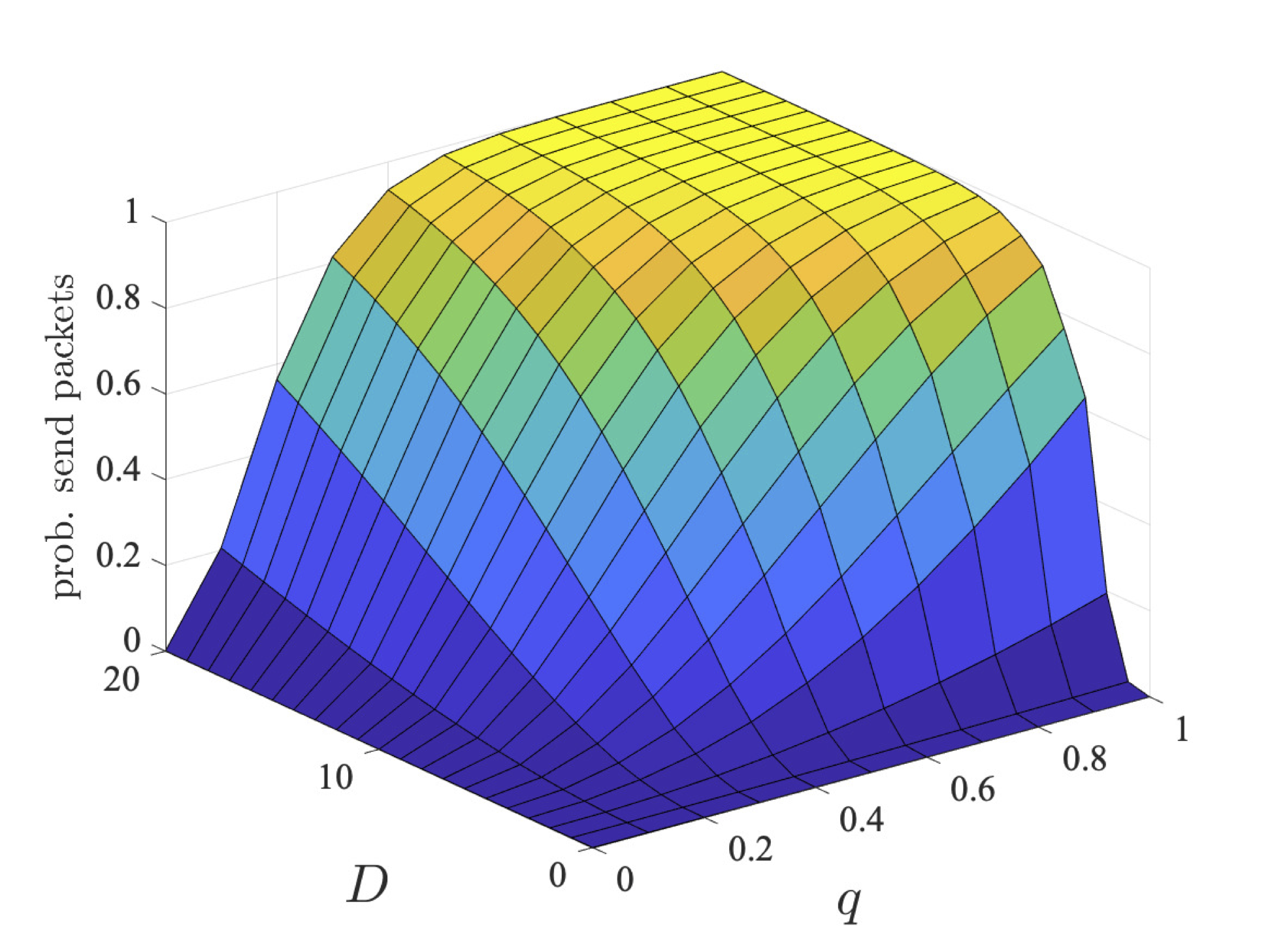
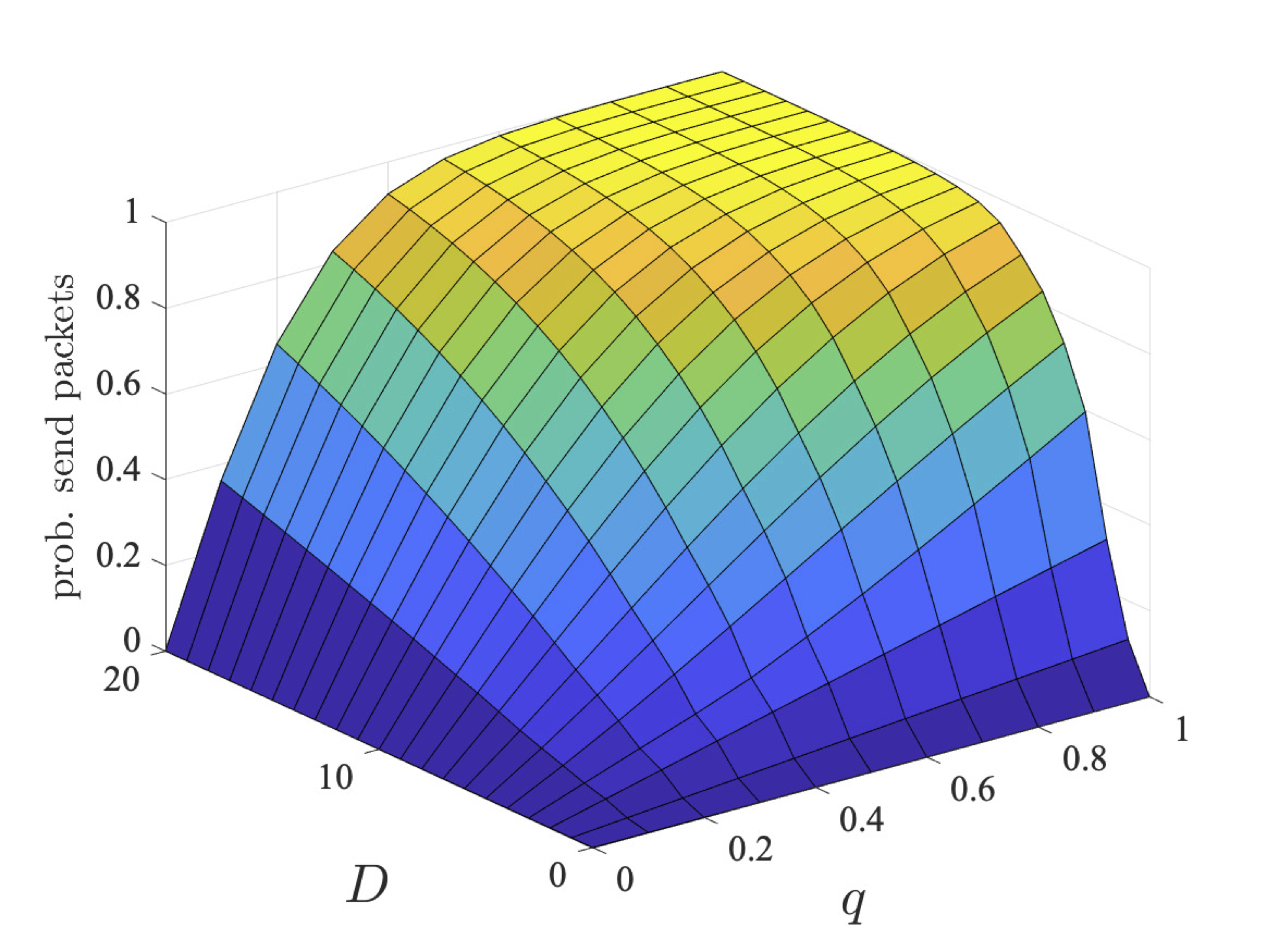
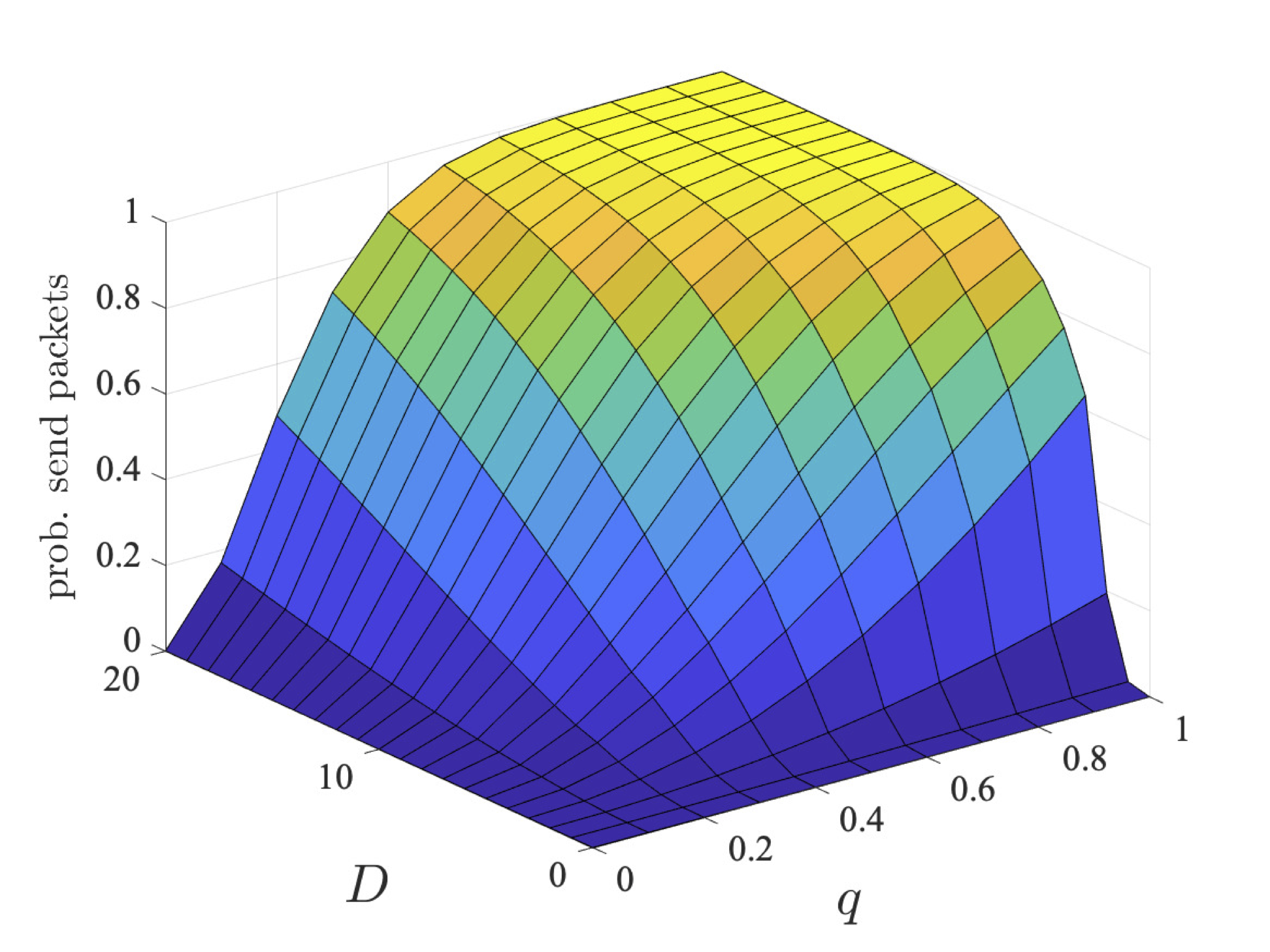
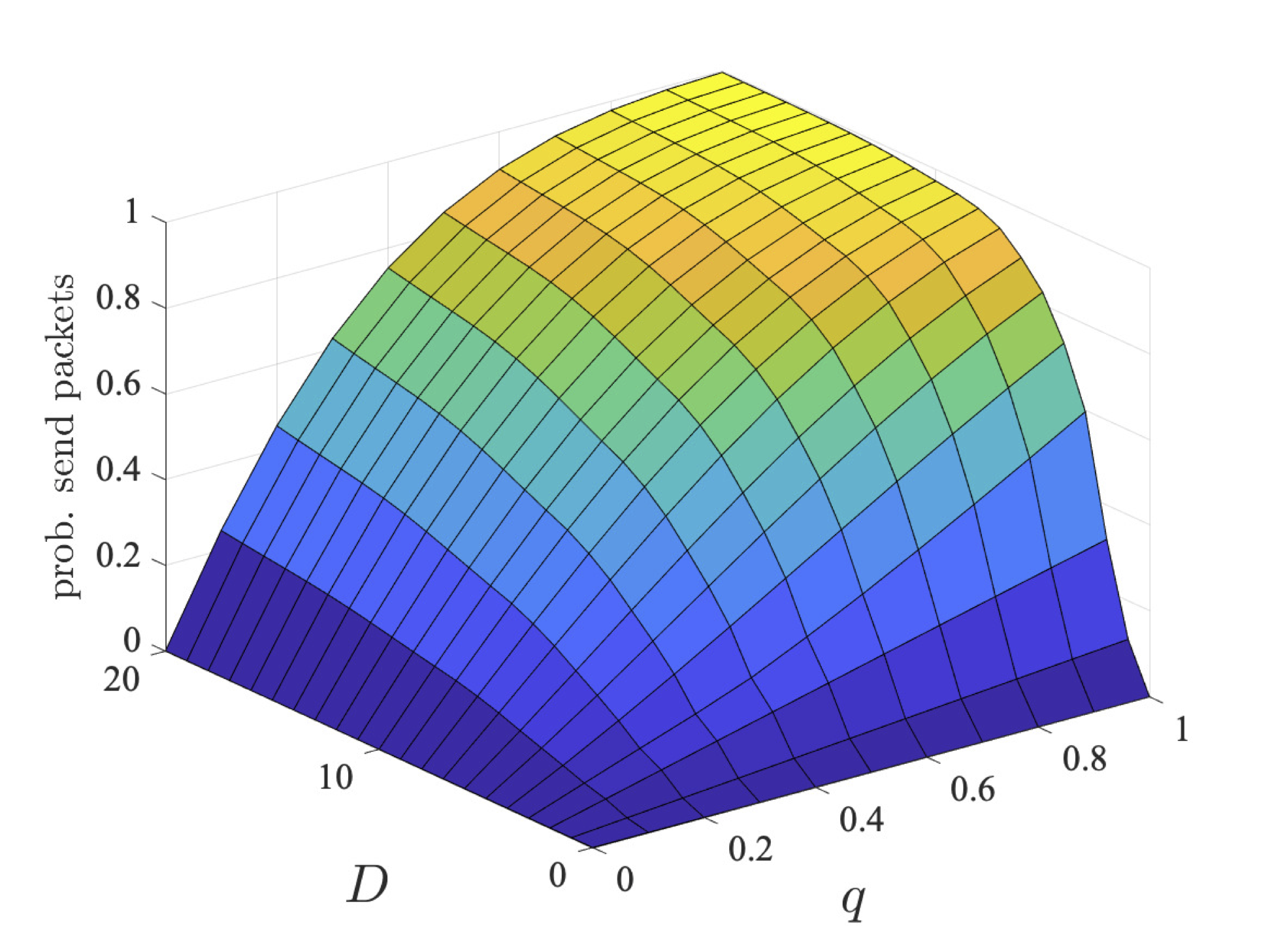
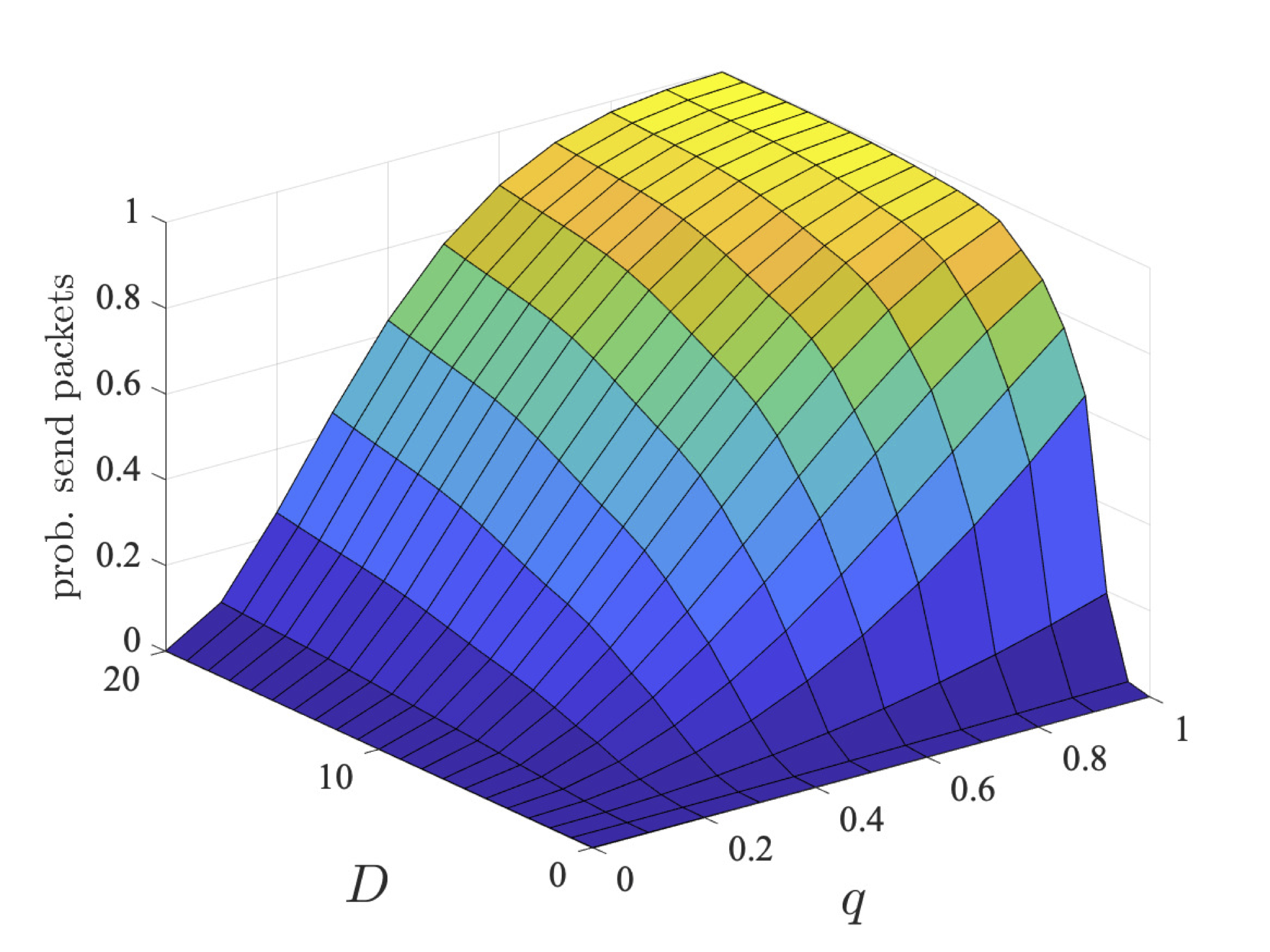
We next consider nonzero-sum properties where two coalitions (the first user in a coalition on its own and the second and third users in a separate coalition) try and reach their individual goals. Again we consider two classes of properties:
// expected time user 1 eventually sends a packet // and users 2 and 3 form a coalition to send their packets <<usr1:usr2,usr3>>min=? (R{"time"}[F s1=3] + R{"time"}[F s2=3 & s3=3]) // probability user 1 eventually sends a packet by a deadline // and users 2 and 3 form a coalition to send their packets by a deadline <<usr1:usr2,usr3>>max=? (P[F (s1=3 & t<=D)] + P[F (s2=3 & s3=3 & t<=D)])
Through strategy synthesis, we find the collaboration is dependent on q and, in the case of deadline properties, D. In particular, given more time (i.e., larger values of D), there is more chance for the users to collaborate sending in different slots. While, if q is large, it is unlikely users need to repeatedly try and send their packets, and therefore again can send in different slots. As the coalition has more messages to send, their probabilities are lower. However, even for two users, the probabilities are different, since, although it is advantageous to collaborate and only one user tries first, if transmission fails, then both users try to send as this is the best option for their individual goals.